Análises estatísticas

Author

Nívia

Tipos de testes para análise estatística

Veremos nesta aula os tipos de análise de acordo com o número e tipo de variáveis independentes (níveis do fator) e também o número de tratamentos ou grupos a serem comparados.

Teste T

O teste t compara DUAS MÉDIAS (2 tratamentos) e mostra se as diferenças entre essas médias são significativas. Como todo teste estatístico, o teste t também tem como produto a medida do valor de p. Ou seja, no final das contas, teremos calculado a probabilidade da diferença encontrada (entre as médias) terem sido por acaso. Existem 2 tipos mais comuns de teste t:

teste t para 2 amostras dependentes (ou pareadas): compara as médias da mesma população em diferentes momentos de tempo (ex.: antes e depois).
teste t para 2 amostras independentes (ou não pareadas): compara as médias de duas populações distintas.

Os termos paramétrico e não-paramétrico referem-se à média e ao desvio-padrão, que são os parâmetros que definem as populações que apresentam distribuição normal. Veremos como trabalahar nessas duas diferentes sutuações.

Dois tratamentos independentes

Situação:Um pesquisador conduziu um experimento com o objetivo de avaliar o efeito de um micronutriente, o magnésio (Mg), adicionado na solução do solo cultivado com plantas de arroz, no manejo de uma doença fúngica. O experimento foi conduzido em delineamento inteiramente casualizado com 10 repetições, sendo cada repetição um vaso de planta. Um dos tratamentos é o chamado controle, ou testemunha, sem o suplemento mineral. O segundo é aquele com o suplemento do Mg na dose de 2 mM. Em cada uma das repetições foi obtido um valor médio do comprimento de lesões em um determinado tempo após a inoculação.

Preparo pré-análise: carregamento de pacotes e importação do conjunto de dados.

library(magrittr) # para usar pipes
library(ggplot2) # para gráficos
library(dplyr)
library(readxl)
library(tidyr)

data_mg <- read_excel("dados-diversos.xlsx")
head(data_mg)

# A tibble: 6 × 3
  trat    rep  comp
  <chr> <dbl> <dbl>
1 Mg2       1   9  
2 Mg2       2  12.5
3 Mg2       3  10  
4 Mg2       4   8  
5 Mg2       5  13.2
6 Mg2       6  11

Agora, vamos começar a trabalhar esses dados e obter estatísticas que descrevem o conjunto de dados, seja a tendência central ou a dispersão dos dados. Neste caso, trabalhamos com a média (mean), variância (var), desvio padrão (sd), erro padrão (se) e intervalo de confiança (ci). O intervalo de confiança é apenas para inferência visual.

data2 <- data_mg %>%
  group_by(trat) %>%
  summarise(
    mean_com = mean(comp),
    sd_comp = sd(comp),
    var_comp = var(comp),
    n = n(),
    se_comp = sd_comp / sqrt(n - 1),
    ci = se_comp * qt(0,025, df = 9))
data2

# A tibble: 2 × 7
  trat    mean_com sd_comp var_comp     n se_comp    ci
  <chr>      <dbl>   <dbl>    <dbl> <int>   <dbl> <dbl>
1 Mg2         10.5    1.54     2.39    10   0.515  -Inf
2 control     15.7    1.27     1.61    10   0.424  -Inf

Visualização: A maneira mais simples é visualizar, no caso de mais de 6 repetições, usando boxplots juntamente com os dados de cada repetição. Aqui visualizaremos os dados em gráfico de barras vertical com erro padrão.

data2 |> 
  ggplot(aes(trat, mean_com)) +
  geom_col(width = 0.5,
           fill = "steelblue") +
  geom_errorbar(aes(
    ymin = mean_com - se_comp,
    ymax = mean_com + se_comp),
    width = 0.1) +
  ylim(0,20) +
labs(x = "", y = "Mean size (mm)")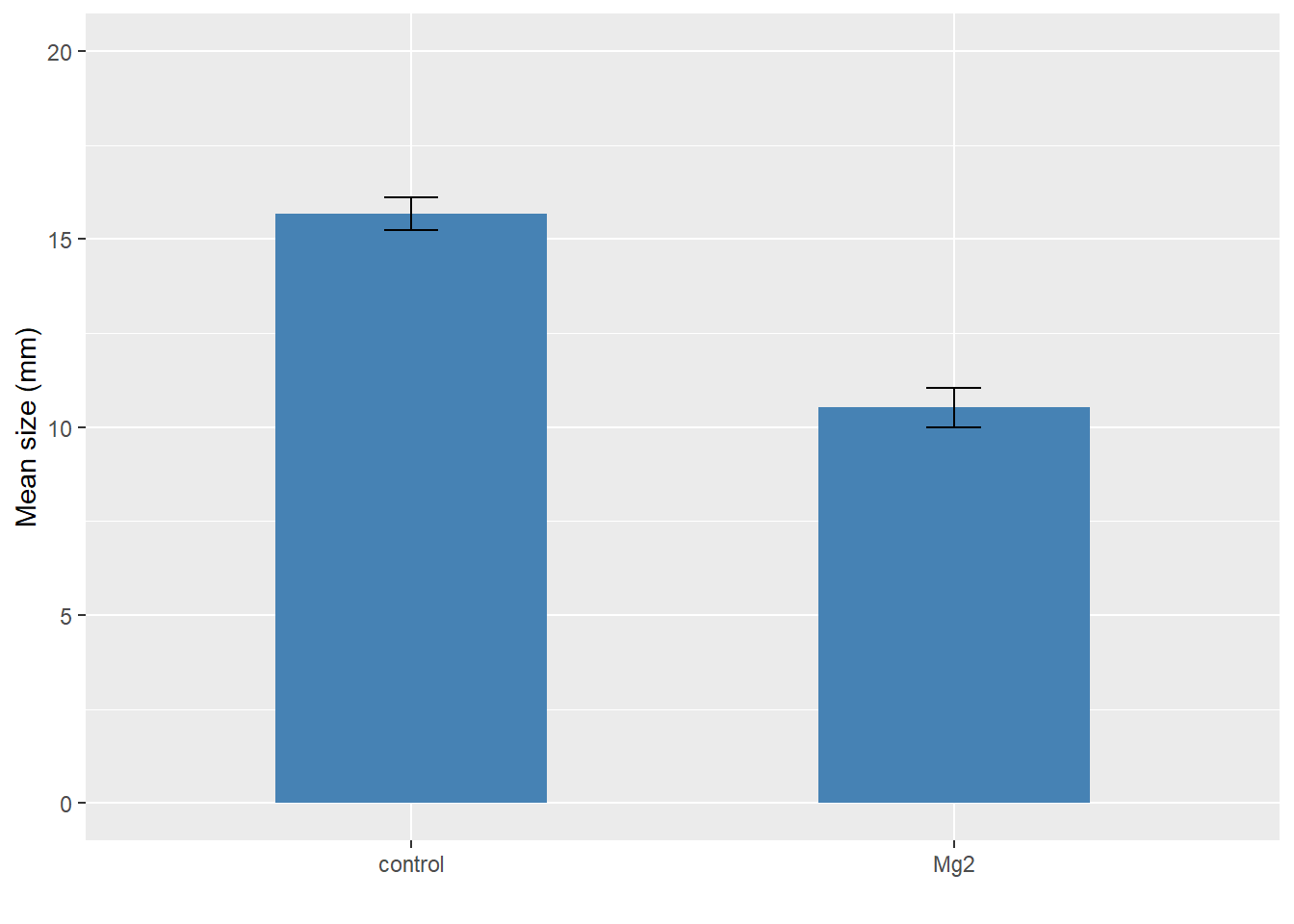

Intervalo de confiança: Agora visualizamos os dados com o ci. Abaixo, as barras verticais representam o intervalo de confiança 95%.

data2 |> 
  ggplot(aes(trat, mean_com)) +
  geom_col(width = 0.5, fill = "steelblue") +
  geom_errorbar(aes(
    ymin = mean_com - ci,
    ymax = mean_com + ci),
    width = 0.1) +
  ylim(0,20) +
labs(x = "", y = "Mean size (mm)")

O conjunto de dados está no formato largo, assim a variável resposta de interesse está apenas em uma coluna. Existem várias formas de separar em dois vetores os dados de resposta para cada tratamento. Uma delas é por meio da função pivot_winder, a qual coloca as respostas em duas colunas, uma para cada tratamento. Para isso, criaremos o conjunto data_mg2. Agora é posspivel visualizar as respostas (tamanho da lesão) para cada tratamento usando o conjunto de dados original, já que O ggplot2 requer os dados no formato largo.

data_mg2 <- data_mg |>
  pivot_wider(1,
              names_from = trat,
              values_from = comp)
data_mg2

# A tibble: 10 × 3
     rep   Mg2 control
   <dbl> <dbl>   <dbl>
 1     1   9      13.7
 2     2  12.5    15.9
 3     3  10      15.7
 4     4   8      14.2
 5     5  13.2    15.9
 6     6  11      16.5
 7     7  10.8    18  
 8     8   9.5    14.4
 9     9  10.8    16.4
10    10  10.4    16

Teste de hipótese - teste t

Teste t é um teste paramétrico e para ele precisa seguir 2 premissas - normalidade e homogeneidade da variância (homocedasticidade). Caso hja necessidade de transformação dos dados para deixá-los normais, é aceitável.

t.test(data_mg2$Mg2, data_mg2$control, 
paired = F)


    Welch Two Sample t-test

data:  data_mg2$Mg2 and data_mg2$control
t = -8.1549, df = 17.354, p-value = 2.423e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.490393 -3.825607
sample estimates:
mean of x mean of y 
   10.520    15.678

A ordem de execução dos testes deve ser: Shapiro.teste (teste de normalidade) > var.test (teste de homocedasticidade) > se p menor que 0,05 > t.test. No caso da variância dar heterogênea, var EQUAL = F. No caso dos dados pareados usa-se o argumento pared = TRUE

Homocedastididade

Podemos confirmar a premissa da homocedasticidade pelo teste F. No caso de dois grupos, a função que pode ser usada é a var.test do R. Vamos usar o formato largo e chamar os dois vetores do conjunto. Verifique o P-valor na saída da análise.

attach(data_mg2)
var.test(Mg2, control)


    F test to compare two variances

data:  Mg2 and control
F = 1.4781, num df = 9, denom df = 9, p-value = 0.5698
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.3671417 5.9508644
sample estimates:
ratio of variances 
          1.478111

A verificação deste pressuposto também pode ser realizada graficamente através do boxplot para os tratamentos vs resíduos. Se existir homocedasticidade espera-se que os boxplots sejam semelhantes.

Normalidade

A normalidade pode ser testada por meio de procedimentos visuais e testes específicos. Para testar a normalidade dos dados, fazemos o teste shapiro.

shapiro.test(Mg2)


    Shapiro-Wilk normality test

data:  Mg2
W = 0.97269, p-value = 0.9146

shapiro.test(control)


    Shapiro-Wilk normality test

data:  control
W = 0.93886, p-value = 0.5404

Análise visual da premissa de normalidade: A análise visual da premissa de normalidade é realizada por qqplot (QQ-Plot), que permite verificar se uma amostra segue uma distribuição gaussiana. Podemos simplesmente fazer usando as funções qqnorm() e qqline() para cada umas das variáveis analisadas.

qqnorm (Mg2)
qqline(Mg2)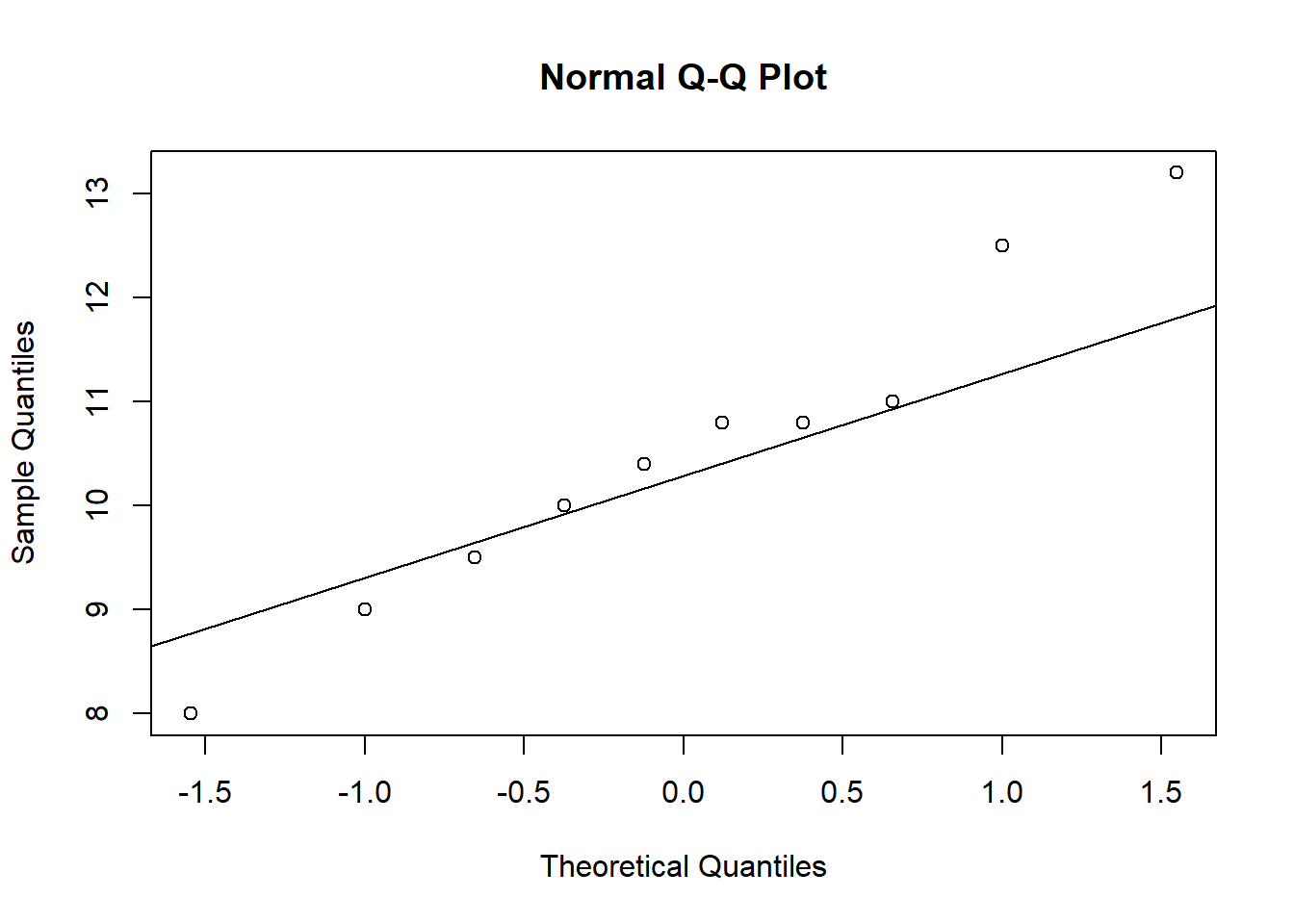

qqnorm(control)
qqline(control)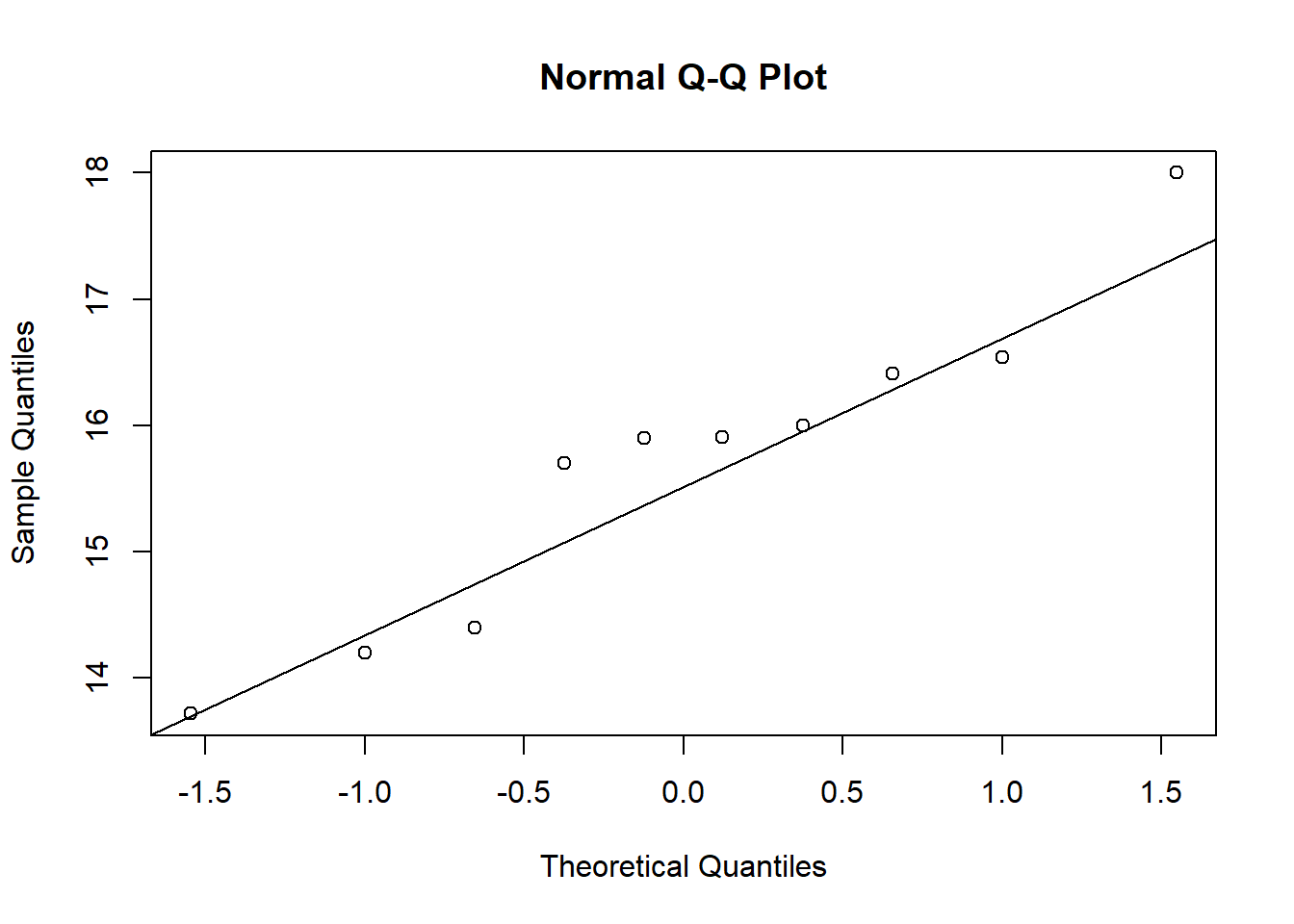

Dois tratamentos dependentes

Se as premissas de normalidade não fossem atendidas, qual o teste que poderia ser usado? Nesse caso de dois grupos há duas possibilidades, uma é usar um teste não paramétrico ou um teste baseado em reamostragem (bootstrapping) dos dados, os quais independem do modelo de distribuição. Vejamos um exemplo.

Situação: Um experimento foi conduzido para avaliar o efeito do uso da escala na acurácia e precisão de avaliações visuais de severidade por avaliadores. A hipótese a ser testada foi que avaliações utilizando uma escala digramática como auxílio são mais acuradas do que sem o uso do auxílio. Dez avaliadores foram escolhidos aleatoriamente e fizeram duas avaliações cada. Cinco variáveis que compõe a medida da concordância das estimativas foram obtidas. Uma vez que as medidas foram repetidas no tempo para cada avaliador, as amostras são do tipo dependentes.

Preparo pré-análise: importação dos dados e preparo do conjunto.

escala <- read_excel("dados-diversos.xlsx", "escala")
head(escala)

# A tibble: 6 × 7
  assessment rater acuracia precisao vies_geral vies_sistematico vies_constante
  <chr>      <chr>    <dbl>    <dbl>      <dbl>            <dbl>          <dbl>
1 Unaided    A        0.809    0.826      0.979            1.19         0.112  
2 Unaided    B        0.722    0.728      0.991            0.922       -0.106  
3 Unaided    C        0.560    0.715      0.783            1.16         0.730  
4 Unaided    D        0.818    0.819      0.999            0.948       -0.00569
5 Unaided    E        0.748    0.753      0.993            1.10         0.0719 
6 Unaided    F        0.695    0.751      0.925            0.802        0.336

escala2 <- escala |> 
  select(assessment, rater, acuracia)
escala3 <- escala2|>
  pivot_wider(1,
              names_from = assessment,
              values_from = acuracia)

Checagem das premissas:

## homocedasticidade dois grupos
attach(escala3)
var.test(Aided1, Unaided)


    F test to compare two variances

data:  Aided1 and Unaided
F = 0.17041, num df = 9, denom df = 9, p-value = 0.01461
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.04232677 0.68605885
sample estimates:
ratio of variances 
         0.1704073

## normalidade
shapiro.test(Aided1)$p.value

[1] 0.4260888

shapiro.test(Unaided)$p.value

[1] 0.1131276

Análise visual da normalidade:

qqnorm(Aided1)
qqline(Aided1)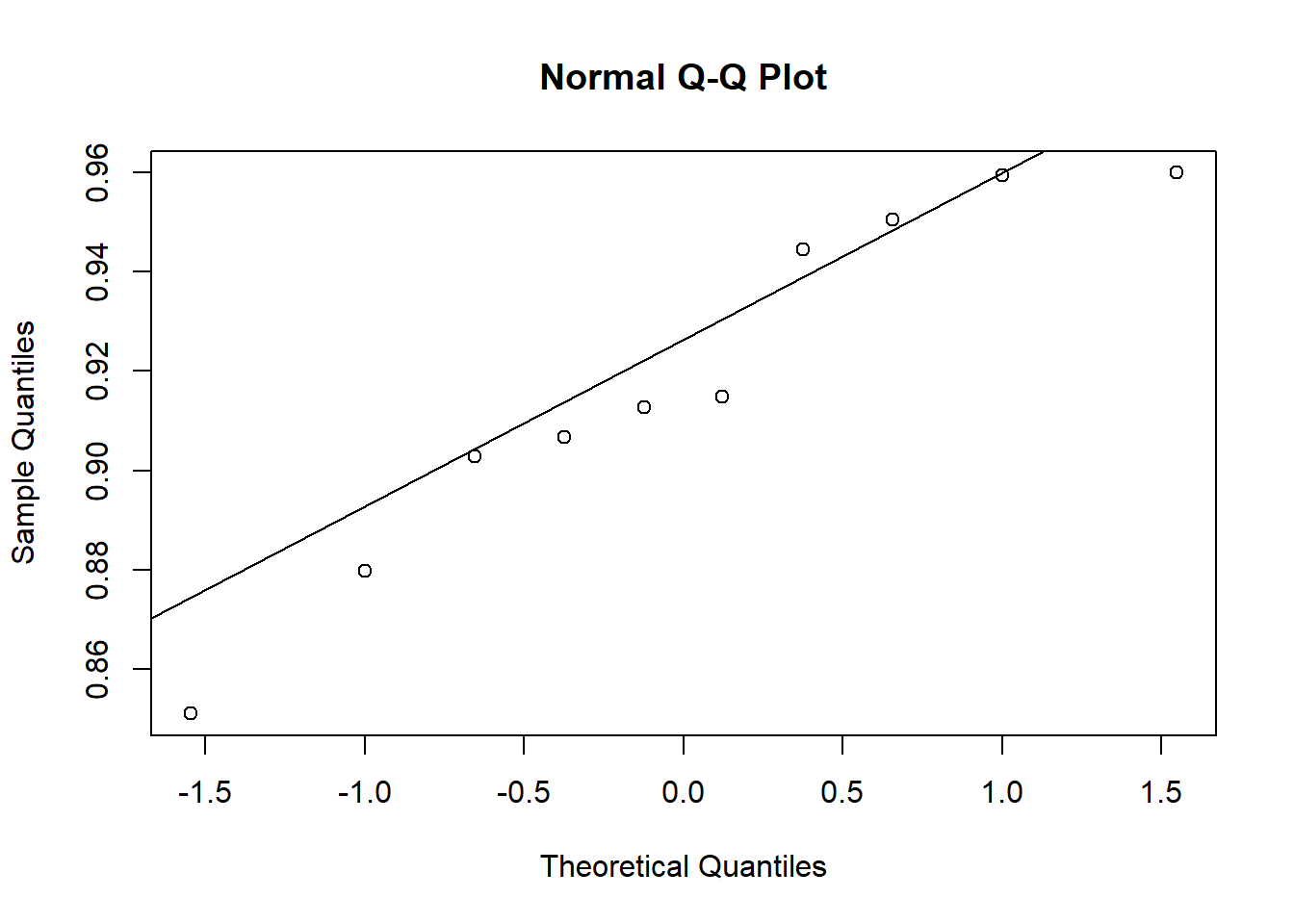

qqnorm(Unaided)
qqline(Unaided)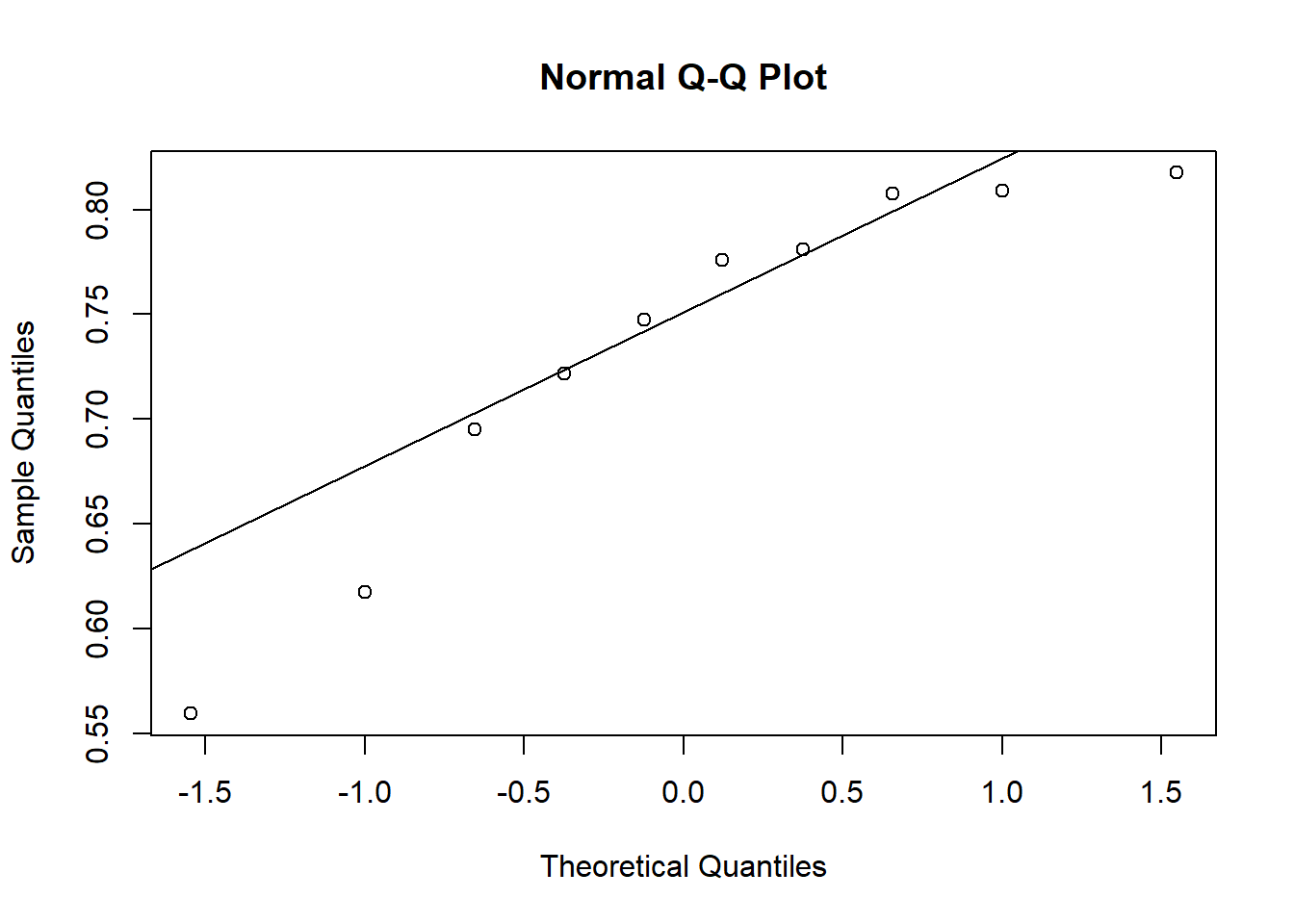

Teste T paramétrico

## teste t para amostras pareadas
t_escala <- t.test(escala3$Aided1, escala3$Unaided,
  paired = TRUE,
  var.equal = F
)

t_escala


    Paired t-test

data:  escala3$Aided1 and escala3$Unaided
t = 5.9364, df = 9, p-value = 0.000219
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 0.1144707 0.2554241
sample estimates:
mean difference 
      0.1849474

Teste para dados não paramétricos

Um teste não paramétrico não faz nenhuma suposição sobre a distribuição da população ou tamanho da amostra. O Wilcox.test é o teste para dados não paramétricos equivalente ao teste t para dados paramétricos. o teste de Wilcoxon é usado para testar se as medianas das amostras são iguais nos casos em que a suposição de normalidade não é satisfeita ou quando não for possível checar essa suposição.

wilcox.test(escala3$Aided1, escala3$Unaided, paired = TRUE)


    Wilcoxon signed rank exact test

data:  escala3$Aided1 and escala3$Unaided
V = 55, p-value = 0.001953
alternative hypothesis: true location shift is not equal to 0