library(tidyverse)
library(readxl)
library(ggplot2)Análise de Correlação
Análise de Correlação
A análise de correlação é usada para avaliar a força e a direção da relação entre duas variáveis contínuas. Ela mede o grau de associação linear entre as variáveis, ou seja, o quanto as variáveis se movem juntas em uma relação linear.
Esta análise permite determinar se as variáveis estão positivamente correlacionadas (quando uma aumenta, a outra também aumenta), negativamente correlacionadas (quando uma aumenta, a outra diminui) ou se não há correlação entre elas. A medida mais comum de correlação é o coeficiente de correlação de Pearson, que varia de -1 a +1. Um valor próximo de +1 indica uma forte correlação positiva, um valor próximo de -1 indica uma forte correlação negativa, e um valor próximo de zero indica uma correlação fraca ou inexistente. A análise de correlação não implica causalidade, apenas indica a presença e a intensidade da relação linear entre as variáveis.
Preparo pré-análise e visualização: Pacotes, conjunto de dados e gráfico.
estande <- read_excel("dados-diversos.xlsx", "estande")
estande |>
ggplot(aes(trat, nplants))+
geom_point()+
facet_wrap(~ exp)+
ylim(0,max(estande$nplants))+
geom_smooth(se = F)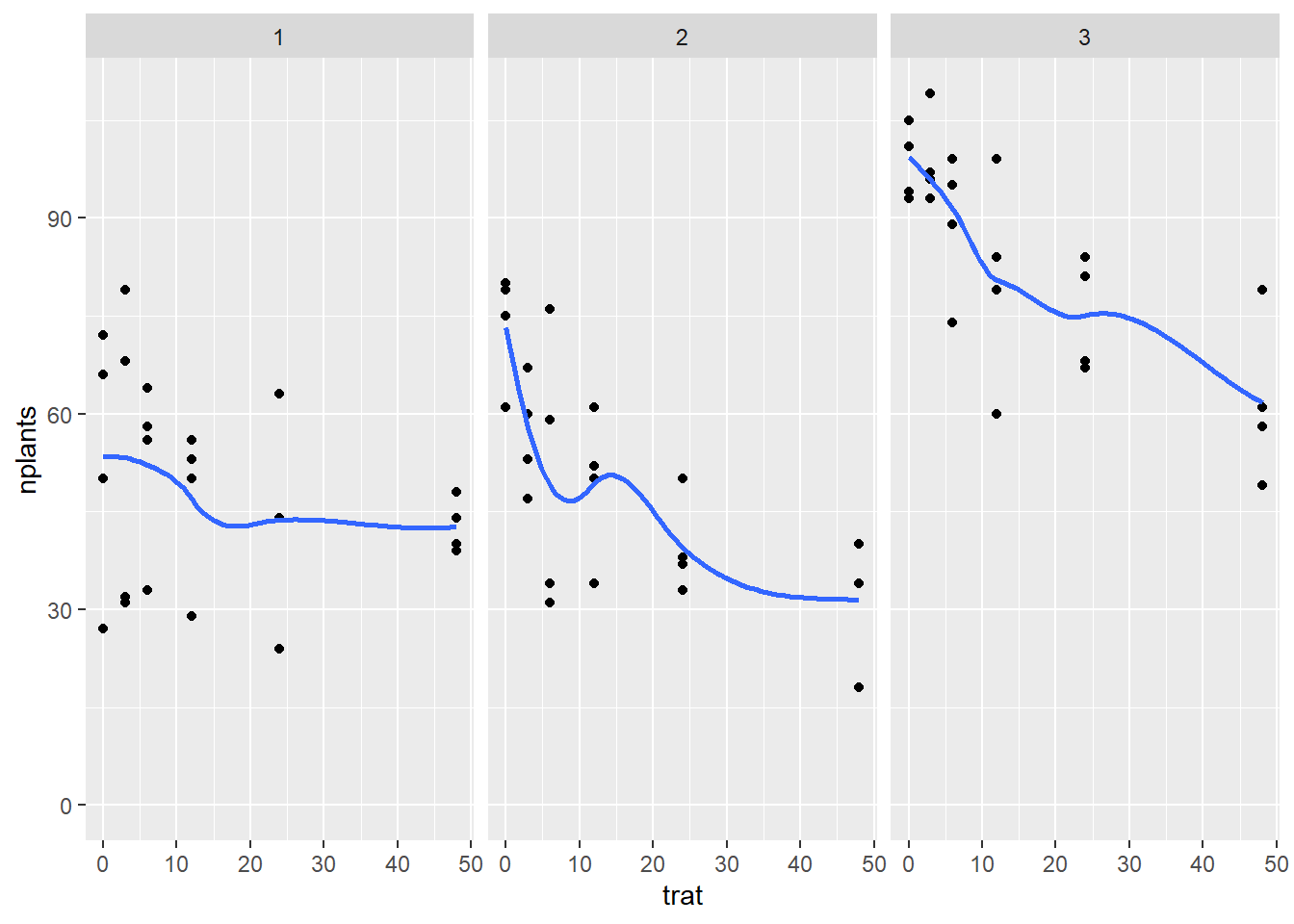
Ajustando modelo linear simples e quadratico
LM: utiliza-se a função lm() para ajustar o modelo linear. Essa função recebe a fórmula do modelo e os dados como argumentos. A fórmula especifica a relação entre a variável dependente e a variável independente. Por exemplo, se sua variável dependente for “y” e sua variável independente for “x”, a fórmula seria y ~ x. A função lm() retornará um objeto do tipo “lm” que representa o modelo ajustado. Usa-se a função summary() para obter uma visão geral dos resultados do modelo ajustado, isso inclui os coeficientes estimados, estatísticas de ajuste (como o coeficiente de determinação R²), valores-p e outros diagnósticos do modelo.
Coeficiente de determinação (R²): o R² representa quanto (em porcentagem) a variável dependente (ou resposta) é explicada pelo modelo de regressão ajustado, ou seja, indica a porcentagem de variação na variável de resposta que pode ser atribuída às variáveis independentes incluídas no modelo. Quanto maior o valor de R², melhor o ajuste do modelo aos dados. O R² varia entre 0 e 1, sendo que o R² igual a 0 indica que o modelo de regressão não é capaz de fornecer uma explicação para a variação nos dados e R² igual a 1 indica que o modelo de regressão oferece uma explicação completa para os dados.
- Ver qual que se adapta melhor.
Filtrar o experimento 2: O group_by vai agrupar pelos tratamentos e o summarise vai dar a média do número de plantas. Se eu quiser seguir a linha em cima dos pontos eu posso colocar o argumento span = 0.7 dentro da função geom_smooth. O R ao quadrado da regressão linear simples é o coeficiente de determinação.
estande2 <- estande |>
filter(exp ==2) |>
group_by(trat) |>
summarise(mean_nplants = mean(nplants))
estande2|>
ggplot(aes(trat, mean_nplants))+
geom_point()+
#geom_line()
geom_smooth(formula = y ~ poly(x, 2), method = "lm", color = "black")+
annotate(geom = "text",
x = 25, y = 70,
label = "y = 66.3 - 1.777x + 0.0222x2
R2 = 0.0.88")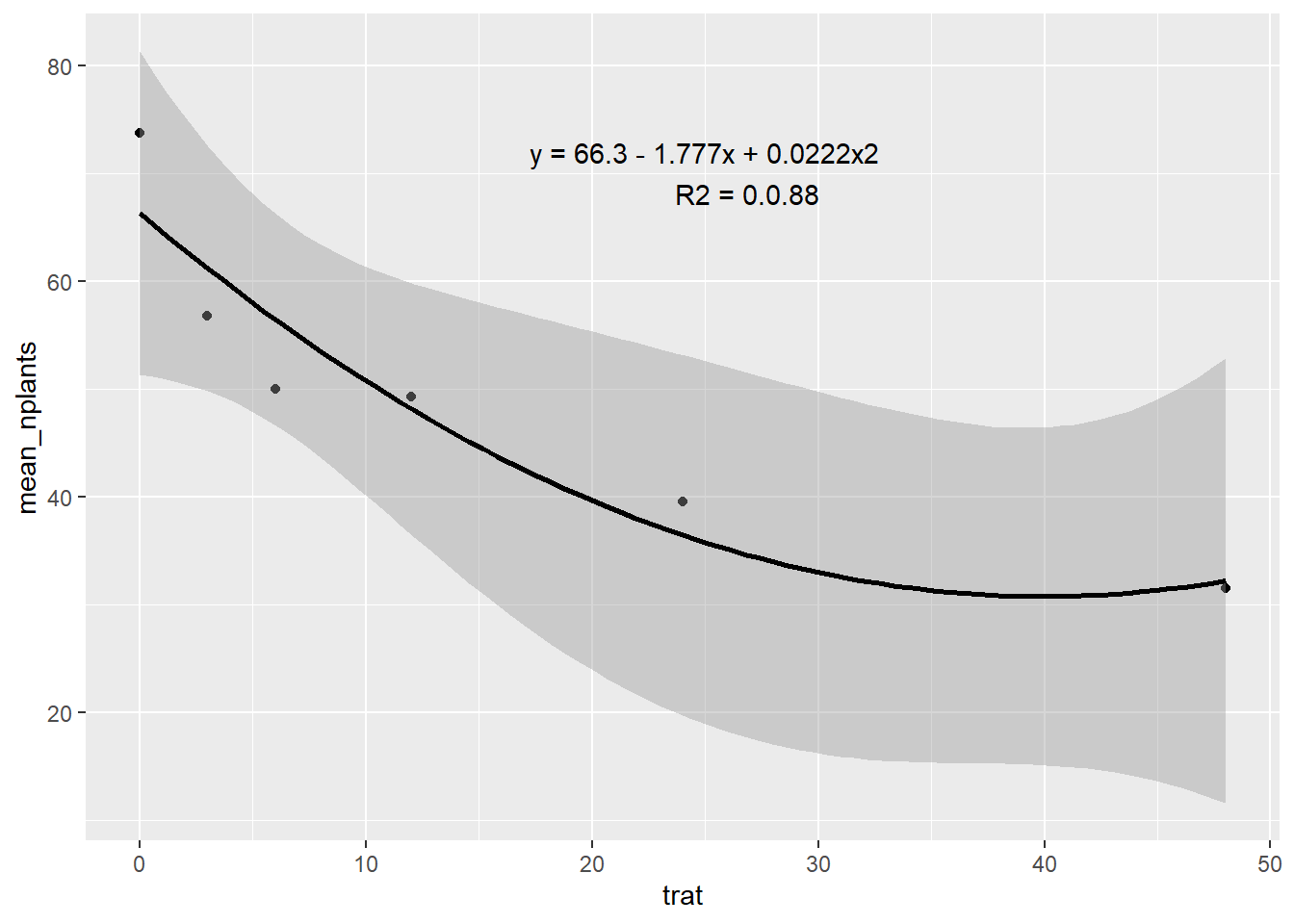
Modelo quadrático: Enquanto a correlação linear mede a associação entre duas variáveis por meio de uma linha reta, a correlação quadrática busca identificar um padrão não linear em forma de curva.
Para ajustar os dados a um modelo linear quadrático, basta utilizar a função lm(). A diferença é que precisará adicionar a variável independente ao quadrado na fórmula do modelo. Por exemplo, se sua variável dependente for “y” e sua variável independente for “x”, a fórmula seria y ~ x + I(x^2). A função I() é usada para indicar uma operação especial, neste caso, elevar “x” ao quadrado. A função lm() retornará um objeto do tipo “lm” que representa o modelo ajustado.
estande2 <- estande2 |>
mutate(trat2 = trat^2)
m1 <- lm(mean_nplants ~ trat, data = estande2)
summary(m1)
Call:
lm(formula = mean_nplants ~ trat, data = estande2)
Residuals:
1 2 3 4 5 6
12.764 -2.134 -6.782 -3.327 -4.669 4.147
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 60.9857 4.5505 13.402 0.000179 ***
trat -0.7007 0.2012 -3.483 0.025294 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 8.117 on 4 degrees of freedom
Multiple R-squared: 0.752, Adjusted R-squared: 0.69
F-statistic: 12.13 on 1 and 4 DF, p-value: 0.02529hist(m1$residuals)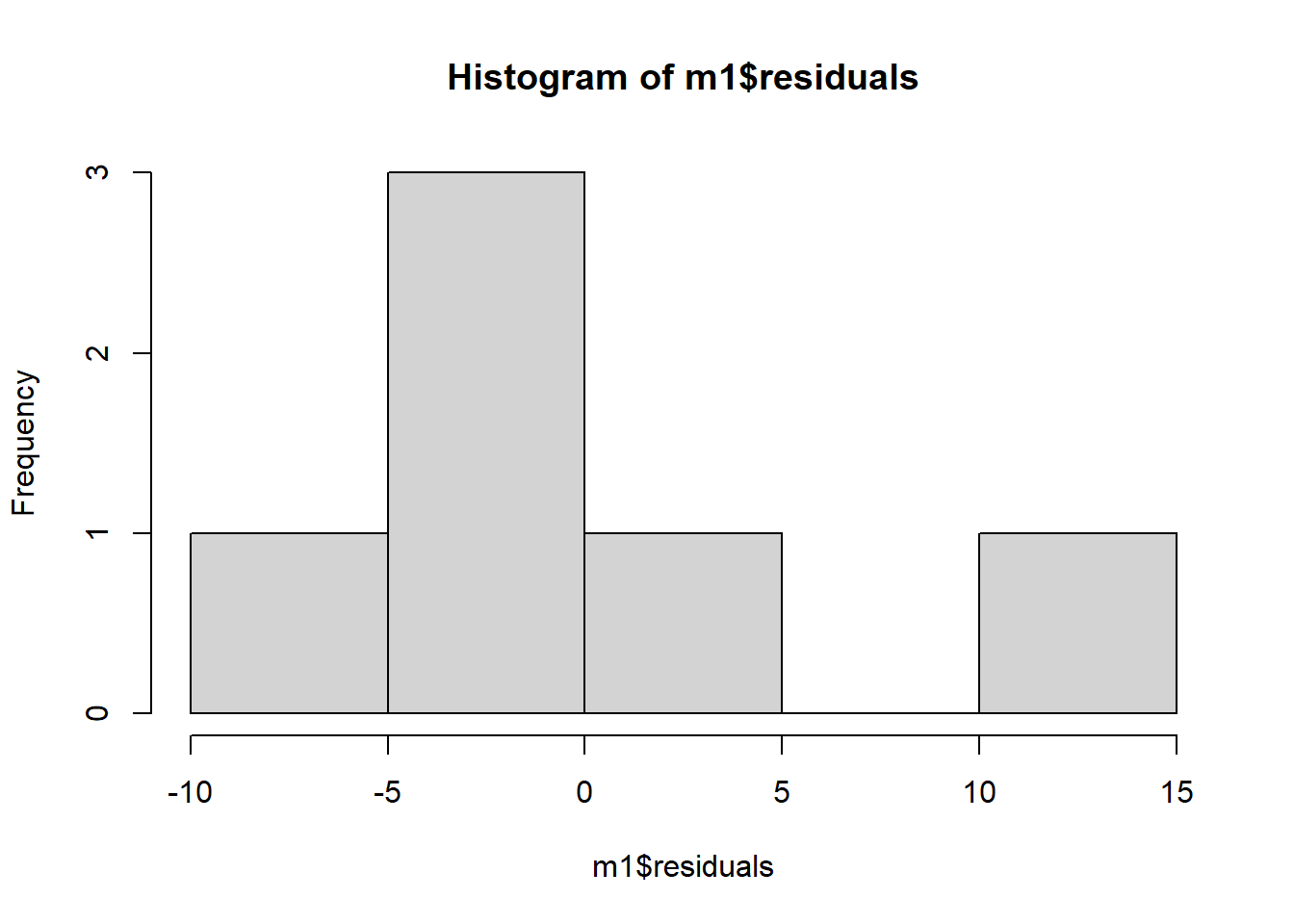
m2 <- lm(mean_nplants ~ trat + trat2,
data = estande2)
summary(m2)
Call:
lm(formula = mean_nplants ~ trat + trat2, data = estande2)
Residuals:
1 2 3 4 5 6
7.4484 -4.4200 -6.4386 1.0739 3.0474 -0.7111
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 66.30156 4.70800 14.083 0.000776 ***
trat -1.77720 0.62263 -2.854 0.064878 .
trat2 0.02223 0.01242 1.790 0.171344
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.517 on 3 degrees of freedom
Multiple R-squared: 0.8801, Adjusted R-squared: 0.8001
F-statistic: 11.01 on 2 and 3 DF, p-value: 0.04152AIC(m1, m2) df AIC
m1 3 45.72200
m2 4 43.36151Duas variáveis resposta
Quando se tem 2 variáveis resposta do tipo numérica contínua, estuda-se a relação das 2 respostas. Na análise de correlação, da-se o coeficiente de correlação de pearson (R). O R² vai ser sempre menor ou igual ao R, pois o R² é obtido elevando o R ao quadrado então, se R for positivo, R² será menor ou igual.
Coeficiente de correlação de Pearson: O coeficiente de correlação de Pearson (R) quantifica a relação linear entre duas variáveis contínuas. Ele mede a direção e a força dessa relação, variando entre -1 e 1.
mofo <- read_excel("dados-diversos.xlsx", "mofo")
mofo |>
ggplot(aes(inc, yld))+
geom_point()+
geom_smooth(se = F, method = "lm")+
facet_wrap(~ study)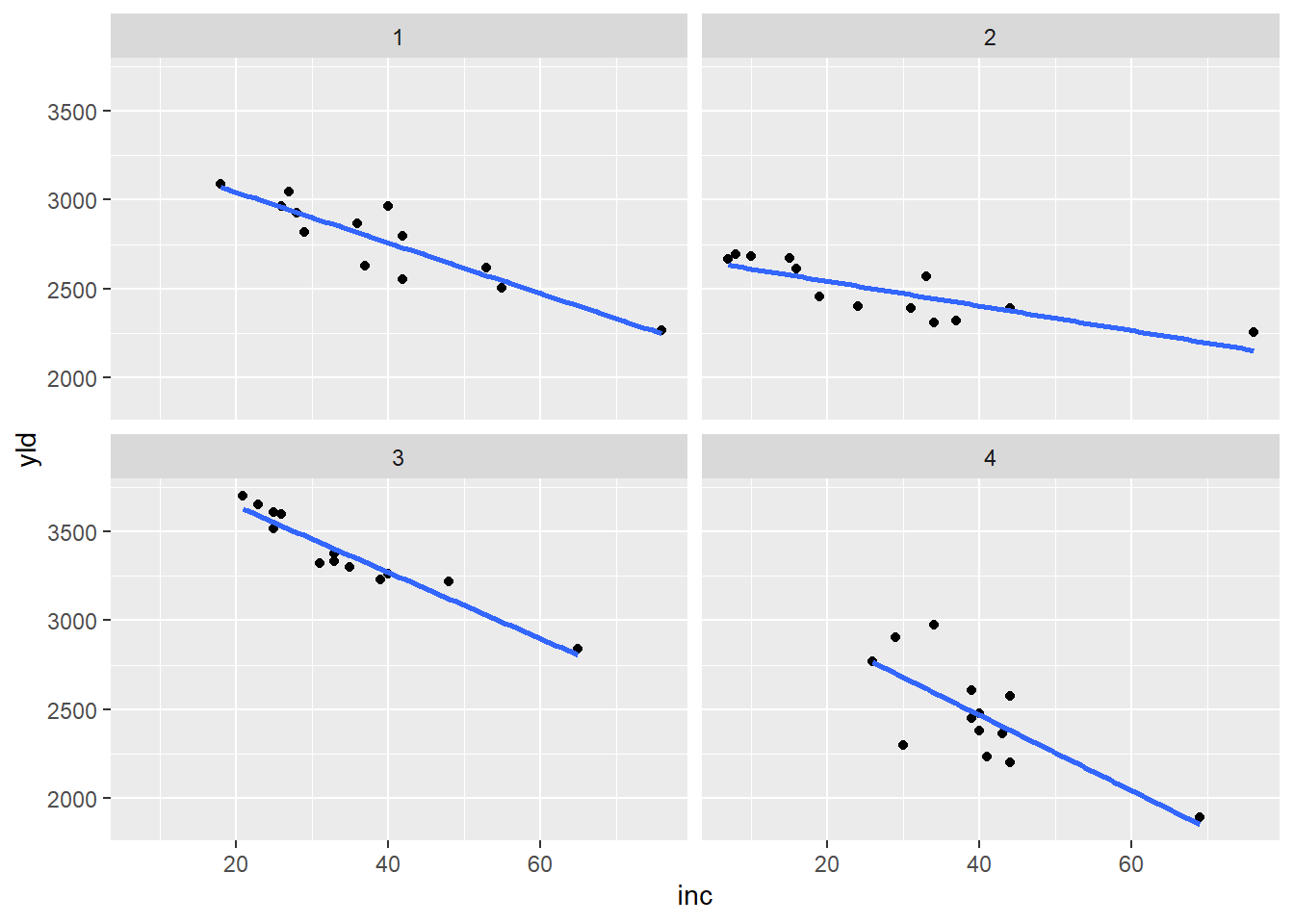
O método de Pearson é sensível a relações lineares, ou seja, ele mede apenas a relação linear entre as variáveis. Se a relação entre as variáveis for não linear, o coeficiente de correlação de Pearson pode não ser uma medida adequada.
Função cor.test: Para calcular o coeficiente de correlação, usa-se a função cor.test(). Essa função além de calcular a correlação, realiza um teste de hipótese para verificar se a correlação é estatisticamente significativa.
Filtrando o experimento 1:
mofo1 <- mofo |>
filter(study ==1)
mofo1# A tibble: 13 × 5
study treat inc scl yld
<dbl> <dbl> <dbl> <dbl> <dbl>
1 1 1 76 2194 2265
2 1 2 53 1663 2618
3 1 3 42 1313 2554
4 1 4 37 1177 2632
5 1 5 29 753 2820
6 1 6 42 1343 2799
7 1 7 55 1519 2503
8 1 8 40 516 2967
9 1 9 26 643 2965
10 1 10 18 400 3088
11 1 11 27 643 3044
12 1 12 28 921 2925
13 1 13 36 1196 2867cor.test(mofo1$inc, mofo1$yld)
Pearson's product-moment correlation
data: mofo1$inc and mofo1$yld
t = -6.8451, df = 11, p-value = 2.782e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9699609 -0.6921361
sample estimates:
cor
-0.8999278 Filtrando o experimento 2:
mofo1 <- mofo |>
filter(study ==2)
mofo1# A tibble: 13 × 5
study treat inc scl yld
<dbl> <dbl> <dbl> <dbl> <dbl>
1 2 1 76 1331 2257
2 2 2 44 756 2393
3 2 3 24 338 2401
4 2 4 33 581 2568
5 2 5 37 588 2320
6 2 6 34 231 2308
7 2 7 31 925 2389
8 2 8 16 119 2614
9 2 9 10 394 2681
10 2 10 8 206 2694
11 2 11 15 275 2674
12 2 12 7 131 2666
13 2 13 19 588 2454cor.test(mofo1$inc, mofo1$yld)
Pearson's product-moment correlation
data: mofo1$inc and mofo1$yld
t = -4.6638, df = 11, p-value = 0.0006894
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9426562 -0.4790750
sample estimates:
cor
-0.8149448 Filtrando o experimento 4 (study = 4):
mofo1 <- mofo |>
filter(study ==4)
mofo1# A tibble: 13 × 5
study treat inc scl yld
<dbl> <dbl> <dbl> <dbl> <dbl>
1 4 1 69 6216 1893
2 4 2 39 2888 2451
3 4 3 41 2272 2232
4 4 4 39 2868 2609
5 4 5 40 2412 2383
6 4 6 40 2372 2480
7 4 7 44 3424 2577
8 4 8 43 1744 2367
9 4 9 26 1456 2769
10 4 10 29 1732 2907
11 4 11 30 1080 2298
12 4 12 34 1592 2976
13 4 13 44 3268 2200cor.test(mofo1$inc, mofo1$yld)
Pearson's product-moment correlation
data: mofo1$inc and mofo1$yld
t = -3.7242, df = 11, p-value = 0.003357
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9194503 -0.3327077
sample estimates:
cor
-0.7467931 Filtrando o experimento 3 (study = 3):
mofo1 <- mofo |>
filter(study ==3)
mofo1# A tibble: 13 × 5
study treat inc scl yld
<dbl> <dbl> <dbl> <dbl> <dbl>
1 3 1 65 5013 2839
2 3 2 33 3619 3375
3 3 3 40 2325 3264
4 3 4 35 2588 3301
5 3 5 48 3969 3220
6 3 6 31 1556 3321
7 3 7 39 3175 3229
8 3 8 25 1763 3517
9 3 9 26 2894 3595
10 3 10 21 350 3702
11 3 11 23 419 3652
12 3 12 25 644 3608
13 3 13 33 2850 3334cor.test(mofo1$inc, mofo1$yld)
Pearson's product-moment correlation
data: mofo1$inc and mofo1$yld
t = -10.9, df = 11, p-value = 3.105e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9872663 -0.8579544
sample estimates:
cor
-0.956692 Matrizes de correlação
Uma matriz de correlação é uma tabela que mostra as correlações entre pares de variáveis. Essa tabela representa as correlações de Pearson (ou outras medidas de correlação) entre as variáveis em um conjunto de dados.
Gerando matriz de correlação para as variáveis selecionadas:
mofo1 <- mofo |>
filter(study ==3)
mofo1# A tibble: 13 × 5
study treat inc scl yld
<dbl> <dbl> <dbl> <dbl> <dbl>
1 3 1 65 5013 2839
2 3 2 33 3619 3375
3 3 3 40 2325 3264
4 3 4 35 2588 3301
5 3 5 48 3969 3220
6 3 6 31 1556 3321
7 3 7 39 3175 3229
8 3 8 25 1763 3517
9 3 9 26 2894 3595
10 3 10 21 350 3702
11 3 11 23 419 3652
12 3 12 25 644 3608
13 3 13 33 2850 3334cor.test(mofo1$inc, mofo1$yld)
Pearson's product-moment correlation
data: mofo1$inc and mofo1$yld
t = -10.9, df = 11, p-value = 3.105e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9872663 -0.8579544
sample estimates:
cor
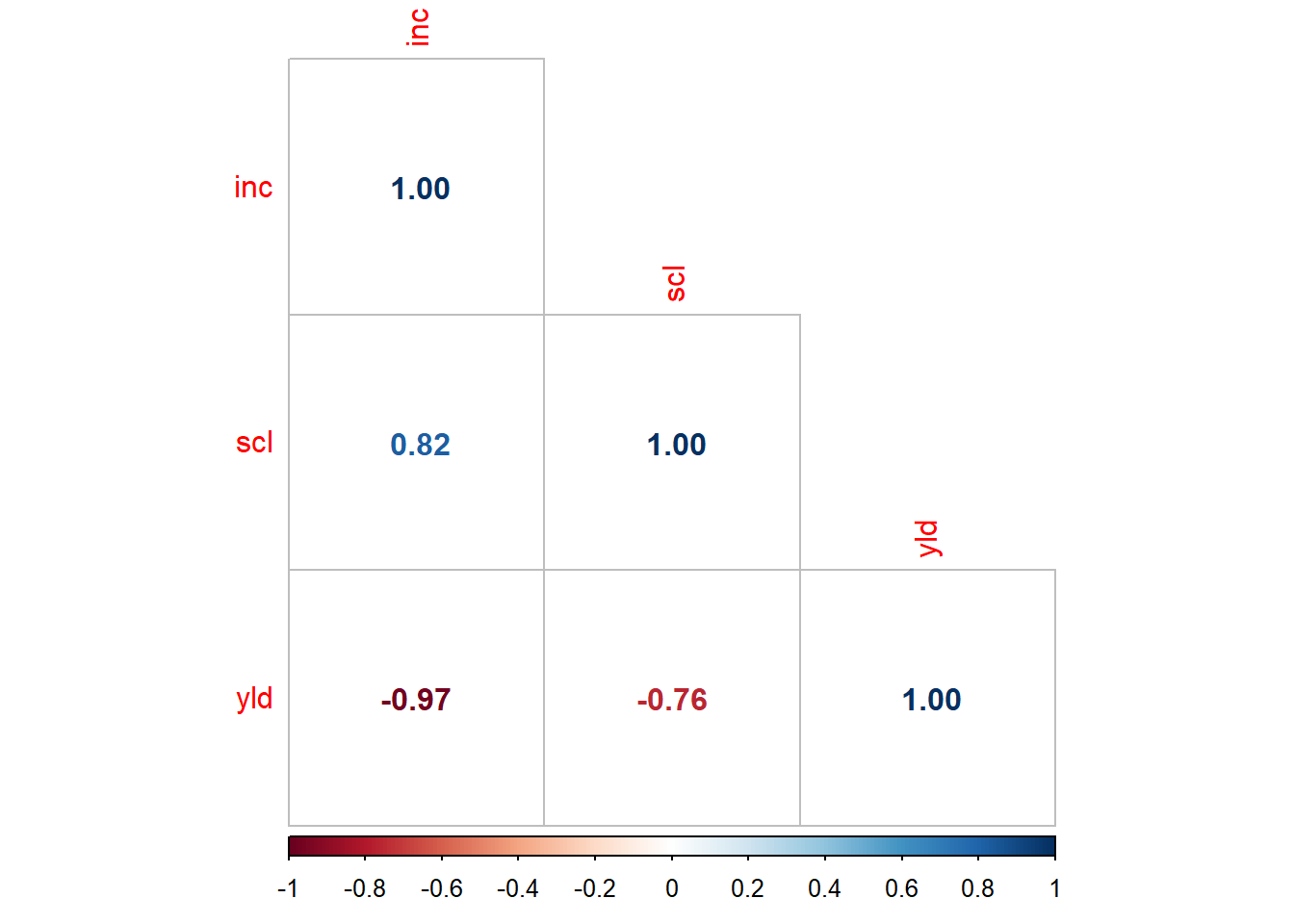
-0.956692 cor(mofo1 |> select(3:5)) inc scl yld
inc 1.0000000 0.8441514 -0.956692
scl 0.8441514 1.0000000 -0.836512
yld -0.9566920 -0.8365120 1.000000Gráficos de correlação
Para gerar gráfico de correlação, usa-se o pacote “corrplot”, que fornece funções para visualizar e analisar matrizes de correlação. Ele é frequentemente usado para explorar a relação entre variáveis e identificar padrões de correlação em conjuntos de dados. Ele oferece uma variedade de gráficos e opções de personalização para representar as correlações de maneira visualmente atraente. Algumas das principais funções deste pacote são: corr.test(): realiza testes estatísticos de correlação para matrizes de correlação, calcula estatísticas de correlação, valores-p e intervalos de confiança para avaliar a significância das correlações. corrplot(): cria uma matriz de plotagem de correlação que permite ajustar diferentes tipos de gráficos, como gráficos de matriz de correlação, gráficos de círculo de correlação, gráficos de barra de correlação etc. Também oferece opções para personalizar cores, adicionar números de correlação e realizar agrupamentos hierárquicos. Existem sete métodos de visualização (parâmetro method) no pacote corrplot, denominados ‘circle’, ‘square’, ‘ellipse’, ‘number’ (números de coeficientes com cores diferentes), ‘shade’, ‘color’, ‘pie’. A intensidade da cor do glifo é proporcional aos coeficientes de correlação por configuração de cor padrão. Existem três tipos de layout (parâmetro type): ‘full’, ‘upper’e ’lower’.
mofo1 <- mofo |>
filter(study ==3)
mofo1# A tibble: 13 × 5
study treat inc scl yld
<dbl> <dbl> <dbl> <dbl> <dbl>
1 3 1 65 5013 2839
2 3 2 33 3619 3375
3 3 3 40 2325 3264
4 3 4 35 2588 3301
5 3 5 48 3969 3220
6 3 6 31 1556 3321
7 3 7 39 3175 3229
8 3 8 25 1763 3517
9 3 9 26 2894 3595
10 3 10 21 350 3702
11 3 11 23 419 3652
12 3 12 25 644 3608
13 3 13 33 2850 3334cor.test(mofo1$inc, mofo1$yld)
Pearson's product-moment correlation
data: mofo1$inc and mofo1$yld
t = -10.9, df = 11, p-value = 3.105e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9872663 -0.8579544
sample estimates:
cor
-0.956692 pcor <- cor(mofo1 |> select(3:5))
library(corrplot)
corrplot(pcor, method = 'number', type = "lower")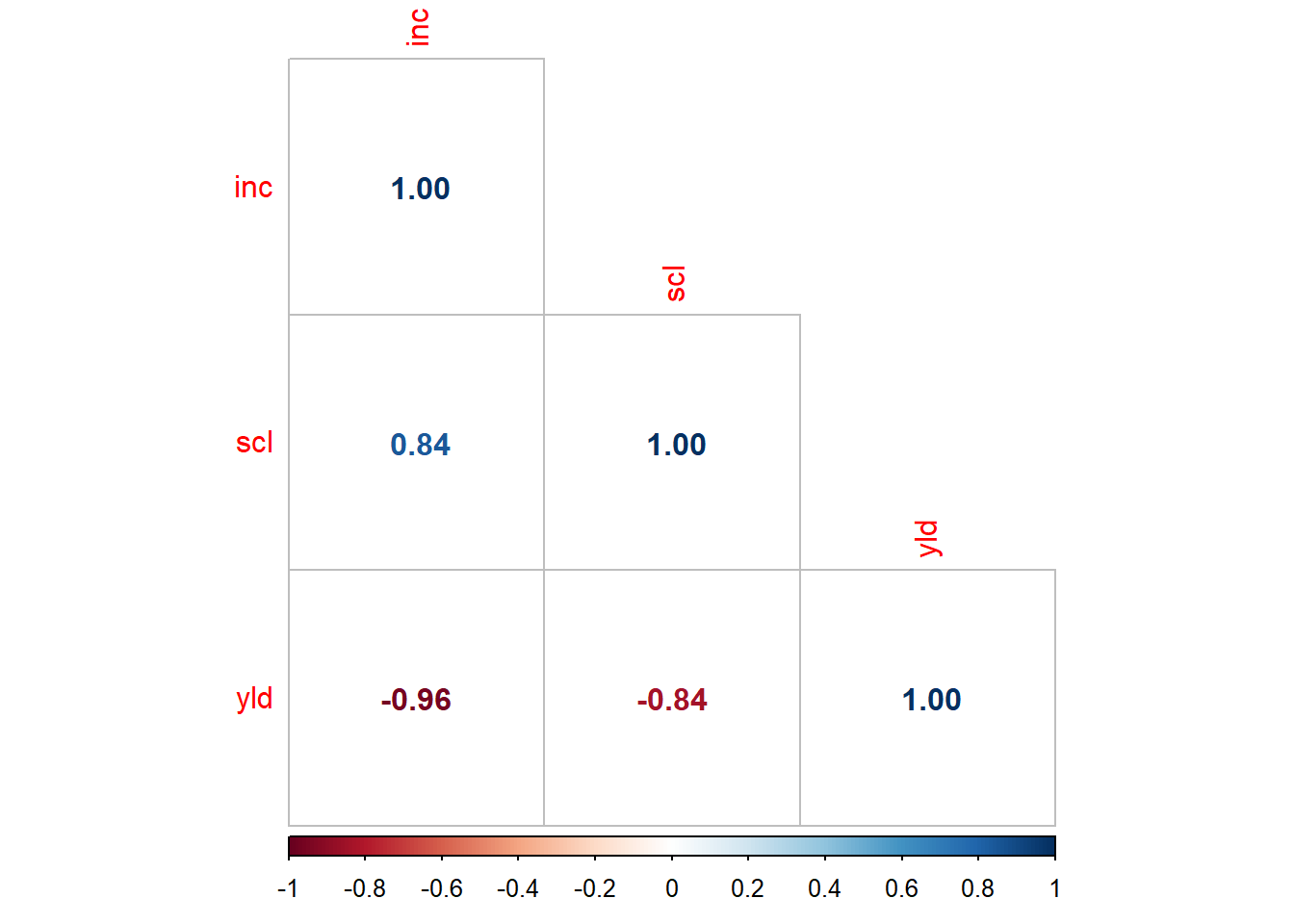
Modelo de Kendall
O modelo de Kendall é uma medida não paramétrica de correlação que avalia a associação entre duas variáveis ordinais ou medidas em escala ordinal. O coeficiente de Kendall também varia de -1 a 1, com interpretações semelhantes ao coeficiente de correlação de Pearson. O método de Kendall é mais robusto do que o método de Pearson para lidar com dados não lineares ou quando a relação entre as variáveis não segue uma distribuição normal.
mofo1 <- mofo |>
filter(study ==3)
mofo1# A tibble: 13 × 5
study treat inc scl yld
<dbl> <dbl> <dbl> <dbl> <dbl>
1 3 1 65 5013 2839
2 3 2 33 3619 3375
3 3 3 40 2325 3264
4 3 4 35 2588 3301
5 3 5 48 3969 3220
6 3 6 31 1556 3321
7 3 7 39 3175 3229
8 3 8 25 1763 3517
9 3 9 26 2894 3595
10 3 10 21 350 3702
11 3 11 23 419 3652
12 3 12 25 644 3608
13 3 13 33 2850 3334shapiro.test(mofo1$inc)
Shapiro-Wilk normality test
data: mofo1$inc
W = 0.87111, p-value = 0.05412shapiro.test(mofo1$yld)
Shapiro-Wilk normality test
data: mofo1$yld
W = 0.92193, p-value = 0.2663cor.test(mofo1$inc, mofo1$yld, method = "spearman")
Spearman's rank correlation rho
data: mofo1$inc and mofo1$yld
S = 715.97, p-value = 7.166e-08
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
-0.9669458 pcor <- cor(mofo1 |> select(3:5), method = "spearman")
library(corrplot)
corrplot(pcor, method = 'number', type = "lower")