Análise de Regressão

Author

Nívia

Dados quantitativos e o uso de análise de regressão

Quando se tem dados quantitativos, a análise de regressão é geralmente mais apropriada do que a análise de variância (ANOVA), pois a análise de regressão permite modelar e prever a relação entre uma variável dependente (Y) e uma ou mais variáveis independentes (X). Ela busca estimar os parâmetros de uma equação de regressão que descreve a relação funcional entre as variáveis. A análise de regressão pode fornecer informações sobre a direção e magnitude do efeito das variáveis independentes na variável dependente, bem como previsões ou estimativas para valores não observados.

Regressão linear simples

Na análise de regressão linear, assume-se que a relação entre a variável dependente e a variável independente é linear, ou seja, pode ser descrita por uma linha reta. A equação da regressão linear é dada por: y = β0 + β1x + ε, onde>: y é a variável dependente (variável resposta), x é a variável independente (tratamento), β0 é o intercepto (ou constante) da equação de regressão, β1 é o coeficiente de inclinação (slope) da equação de regressão e ε é o erro aleatório.

Na regressão linear simples, testamos a hipótese de que a reta de regressão (linha de melhor ajuste), que representa a relação entre as variáveis independentes e a variável dependente, tem um coeficiente de inclinação diferente de zero. Ou seja, testamos a hipótese de que a inclinação da reta de regressão é significativamente diferente de zero (testa se o p valor é diferente de 0).

Preparo pré-análise:

library(tidyverse)
library(readxl)
library(ggplot2)

Conjunto de dados estande (dados-diversos): Visualização em ggplot Para ajustar para uma regressão linear usa-se o argumento method = “lm” dentro da função geom_smooth.

estande <- read_excel("dados-diversos.xlsx", "estande")
estande |>
  ggplot(aes(trat, nplants))+
  geom_point()+
  facet_wrap(~ exp)+
  geom_smooth(se =  F, method = "lm")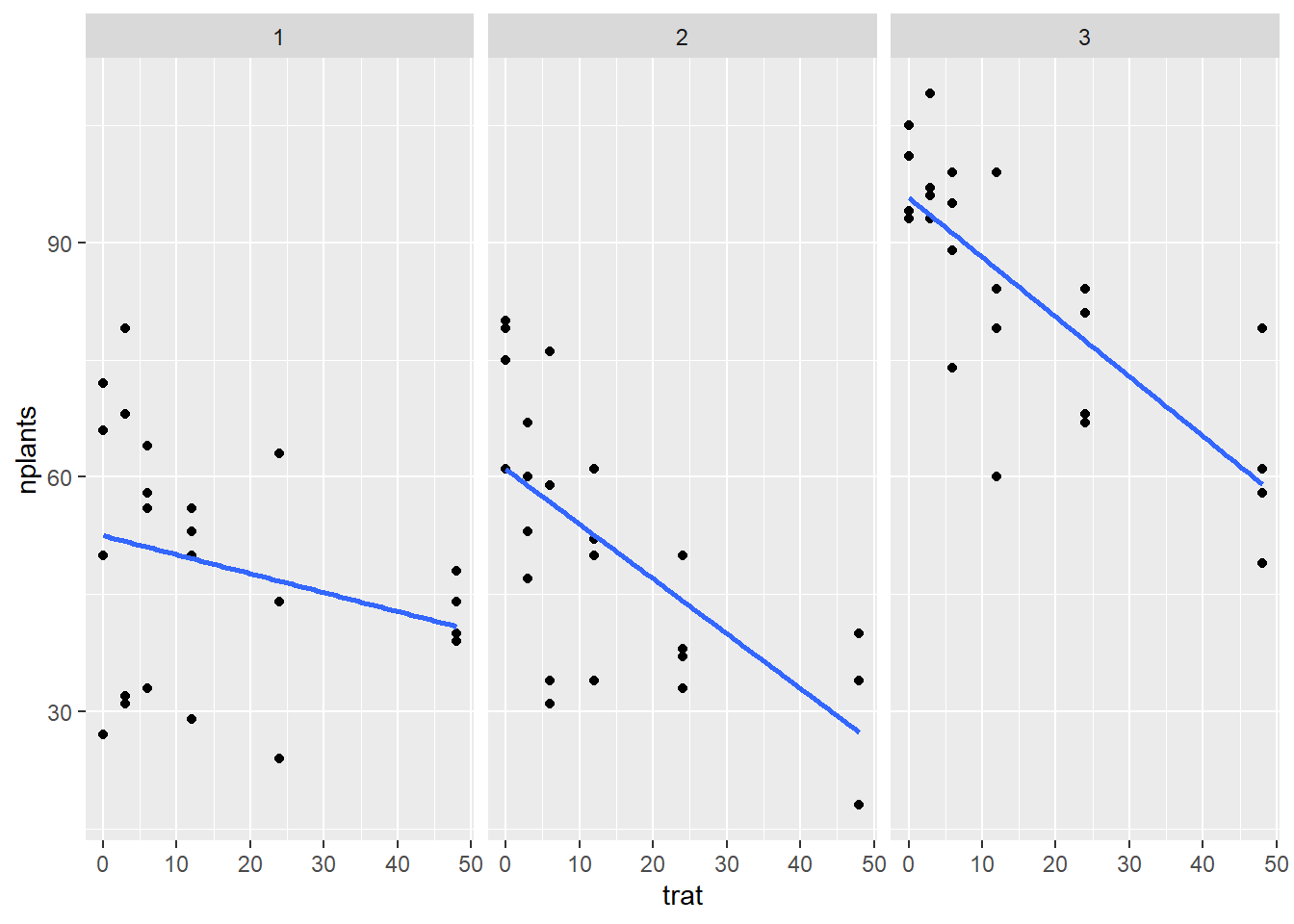

Modelo de melhor ajuste

Posteriomente, deve-se testar o modelo que melhor se ajusta aos dados.Pode-se testar fazer a análise de regressão para cada experimento (isola cada experimento) ou analisar em grupos (modelos mistos).

Analisando cada experimento isoladamente Para isso, cria um novo objeto para os dados (exp1) e atribui estande a ele, depois deve-se filtrar o experimento que deseja e criar um objeto para esse conjunto para viabilizar a realização da análise de regressão.

Exp 1:

exp1 <- estande |>
  filter(exp == 1)

m1 <- lm(nplants ~trat, data = exp1)
summary(m1)


Call:
lm(formula = nplants ~ trat, data = exp1)

Residuals:
    Min      1Q  Median      3Q     Max 
-25.500  -6.532   1.758   8.573  27.226 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  52.5000     4.2044  12.487 1.84e-11 ***
trat         -0.2419     0.1859  -1.301    0.207    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 15 on 22 degrees of freedom
Multiple R-squared:  0.07148,   Adjusted R-squared:  0.02928 
F-statistic: 1.694 on 1 and 22 DF,  p-value: 0.2066

O valor do intercept e o valor de trat (slope) são utilizados na tabela. Intercept é o valor da variável dependente quando a variável independente é igual a zero. Já o slope é a medida da inclinação da linha de regressão, que representa a mudança na variável dependente associada a uma mudança na variável independente.

Para o experimento 2:

exp2 <- estande |>
  filter(exp == 2)

m2 <- lm(nplants ~trat, data = exp2)
summary(m2)


Call:
lm(formula = nplants ~ trat, data = exp2)

Residuals:
     Min       1Q   Median       3Q      Max 
-25.7816  -7.7150   0.5653   8.1929  19.2184 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  60.9857     3.6304  16.798 4.93e-14 ***
trat         -0.7007     0.1605  -4.365 0.000247 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 12.95 on 22 degrees of freedom
Multiple R-squared:  0.4641,    Adjusted R-squared:  0.4398 
F-statistic: 19.05 on 1 and 22 DF,  p-value: 0.0002473

Para o exp3:

exp3 <- estande |>
  filter(exp == 3)

m3 <- lm(nplants ~trat, data = exp3)
summary(m3)


Call:
lm(formula = nplants ~ trat, data = exp3)

Residuals:
     Min       1Q   Median       3Q      Max 
-26.5887  -3.9597   0.7177   5.5806  19.8952 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  95.7500     2.9529  32.425  < 2e-16 ***
trat         -0.7634     0.1306  -5.847 6.97e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 10.53 on 22 degrees of freedom
Multiple R-squared:  0.6085,    Adjusted R-squared:  0.5907 
F-statistic: 34.19 on 1 and 22 DF,  p-value: 6.968e-06

library(report)
report(m3)

We fitted a linear model (estimated using OLS) to predict nplants with trat
(formula: nplants ~ trat). The model explains a statistically significant and
substantial proportion of variance (R2 = 0.61, F(1, 22) = 34.19, p < .001, adj.
R2 = 0.59). The model's intercept, corresponding to trat = 0, is at 95.75 (95%
CI [89.63, 101.87], t(22) = 32.43, p < .001). Within this model:

  - The effect of trat is statistically significant and negative (beta = -0.76,
95% CI [-1.03, -0.49], t(22) = -5.85, p < .001; Std. beta = -0.78, 95% CI
[-1.06, -0.50])

Standardized parameters were obtained by fitting the model on a standardized
version of the dataset. 95% Confidence Intervals (CIs) and p-values were
computed using a Wald t-distribution approximation.

Gráfico para representar a regressão - Para unir os 3 graficos, usa o patchwork.

g1 <- exp1 |>
  ggplot(aes(trat, nplants))+
  geom_point()+
  geom_smooth(method = "lm", se = F)+
  annotate(geom = "text", x = 24,
           y = 70, label = "y = 52.5 - 0.24x")

g2 <- exp2 |>
  ggplot(aes(trat, nplants))+
  geom_point()+
  geom_smooth(method = "lm", se = F)+
  annotate(geom = "text", x = 24,
           y = 70, label = "y = 60 - 0.07x")
g3 <- exp3 |>
  ggplot(aes(trat, nplants))+
  geom_point()+
  geom_smooth(method = "lm", se = F)+
  annotate(geom = "text", x = 24,
           y = 70, label = "y = 95 - 0.07x")

library(patchwork)
g1|g2|g3

Modelo misto

Em um modelo misto, as observações são divididas em grupos ou subgrupos. Cada grupo pode ter um conjunto diferente de efeitos aleatórios e/ou fixos, dependendo da estrutura dos dados. Por exemplo, se os dados foram coletados em diferentes locais geográficos, podemos ter um efeito aleatório para cada local (como no caso do conjunto de dados estande).

Equação: b1 - b2x - cx2

library(lme4)
mix <- lmer(nplants ~trat + (trat | exp),
            data = estande)
summary(mix)

Linear mixed model fit by REML ['lmerMod']
Formula: nplants ~ trat + (trat | exp)
   Data: estande

REML criterion at convergence: 580.8

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-2.0988 -0.6091  0.1722  0.6360  1.9963 

Random effects:
 Groups   Name        Variance  Std.Dev. Corr 
 exp      (Intercept) 510.68405 22.5983       
          trat          0.05516  0.2349  -0.82
 Residual             167.91303 12.9581       
Number of obs: 72, groups:  exp, 3

Fixed effects:
            Estimate Std. Error t value
(Intercept)  69.7452    13.2146   5.278
trat         -0.5687     0.1643  -3.462

Correlation of Fixed Effects:
     (Intr)
trat -0.731
optimizer (nloptwrap) convergence code: 0 (OK)
Model failed to converge with max|grad| = 0.00274249 (tol = 0.002, component 1)

library(car)
Anova(mix)

Analysis of Deviance Table (Type II Wald chisquare tests)

Response: nplants
      Chisq Df Pr(>Chisq)    
trat 11.985  1  0.0005362 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Quando se usa o modelo misto, considera que todos os experimentos são agrupados, então considera que amostra é aleatória. Para fazer o modelo de regressão em grupo (misto) acrescenta-se na função aestetic o argumento group = exp.

estande <- read_excel("dados-diversos.xlsx", "estande")
estande |>
  ggplot(aes(trat, nplants, group = exp))+
  geom_point()+
  #facet_wrap(~ exp)+
  geom_smooth(se =  F, method = "lm")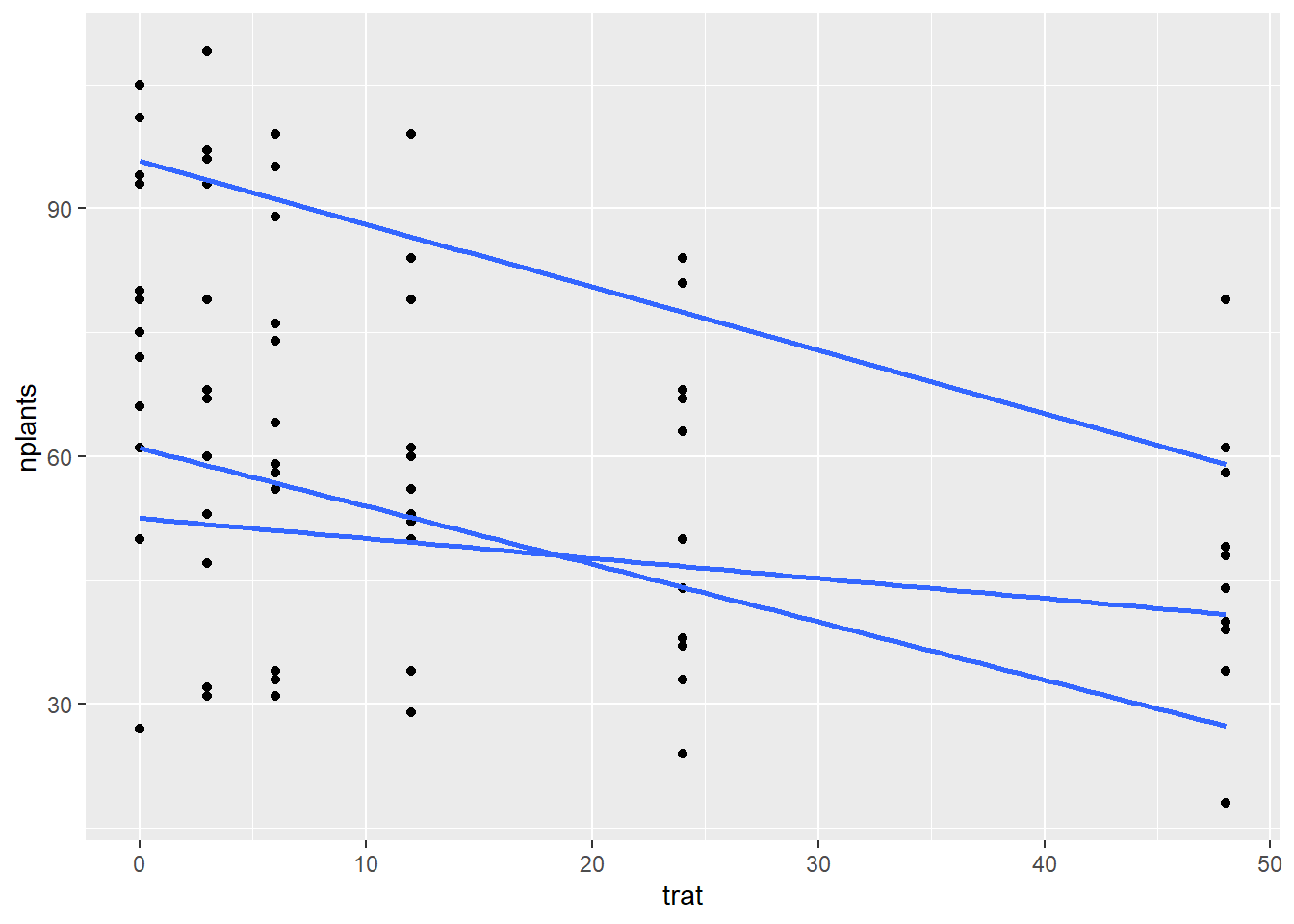

Em geral, os modelos mistos são mais poderosos do que os modelos que tratam cada experimento isoladamente, pois levam em conta a variação tanto entre quanto dentro dos experimentos. Além disso, os modelos mistos permitem que os dados sejam analisados em sua totalidade, sem perder informações importantes sobre a estrutura dos dados.

Modelo GLM

O modelo linear generalizado é uma alternativa ao modelo linear. O GLM é considerado uma extensão do modelo linear que permite acomodar uma variedade de tipos de variáveis resposta, incluindo variáveis categóricas e contínuas. Além disso, o modelo linear generalizado permite que a relação entre a variável resposta e as variáveis explicativas seja não-linear. Ou seja, ele não se limita à suposição de que a relação é uma linha reta.

lm1 <- lm(nplants ~ trat, data = exp3)
summary(lm1)


Call:
lm(formula = nplants ~ trat, data = exp3)

Residuals:
     Min       1Q   Median       3Q      Max 
-26.5887  -3.9597   0.7177   5.5806  19.8952 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  95.7500     2.9529  32.425  < 2e-16 ***
trat         -0.7634     0.1306  -5.847 6.97e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 10.53 on 22 degrees of freedom
Multiple R-squared:  0.6085,    Adjusted R-squared:  0.5907 
F-statistic: 34.19 on 1 and 22 DF,  p-value: 6.968e-06

glm1 <- glm(nplants ~ trat, family = "gaussian",
            data = exp3)

glm2 <- glm(nplants ~ trat, family = poisson(link = "log"),
            data = exp3)
AIC(glm1)

[1] 185.0449

AIC(glm2)

[1] 183.9324

summary(glm1)


Call:
glm(formula = nplants ~ trat, family = "gaussian", data = exp3)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-26.5887   -3.9597    0.7177    5.5806   19.8952  

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  95.7500     2.9529  32.425  < 2e-16 ***
trat         -0.7634     0.1306  -5.847 6.97e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for gaussian family taken to be 110.9787)

    Null deviance: 6235.8  on 23  degrees of freedom
Residual deviance: 2441.5  on 22  degrees of freedom
AIC: 185.04

Number of Fisher Scoring iterations: 2

summary(glm2)


Call:
glm(formula = nplants ~ trat, family = poisson(link = "log"), 
    data = exp3)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-2.94600  -0.46988   0.02453   0.61868   2.34657  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)  4.571590   0.029539 154.762  < 2e-16 ***
trat        -0.009965   0.001488  -6.697 2.13e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 77.906  on 23  degrees of freedom
Residual deviance: 29.952  on 22  degrees of freedom
AIC: 183.93

Number of Fisher Scoring iterations: 4

O modelo linear generalizado com distribuição gaussiana (family = gaussian) é usado quando a variável resposta é contínua e tem uma distribuição normal, ou seja, o mesmo que “lm”. Já o modelo linear generalizado com distribuição de Poisson é usado quando a variável resposta é um número inteiro e não negativo e segue uma distribuição de Poisson (family = poisson). O AIC (Akaike’s Information Criterion) é um critério de seleção de modelo usado para escolher o melhor modelo entre vários modelos candidatos. A escolha do modelo com o menor AIC é importante porque ele é uma medida de qualidade do modelo que leva em consideração tanto o ajuste aos dados quanto a complexidade do modelo. Como o AIC de menor valor é melhor, a família poisson é o ideal para os dados analisados.