Tabela de contingência e AUDPC

Author

Nívia

Variáveis categóricas e tabelas de contingência

No caso de variáveis resposta categóricas, não se tira a média dos dados, ao invés disso, se monta uma tabela de contigência. As tabelas são usadas para resumir e apresentar a distribuição conjunta de duas ou mais variáveis categóricas. Elas são muito úteis para analisar a relação entre essas variáveis e identificar possíveis associações ou dependências.

As tabelas de contingência são bastante utilizadas em estatística descritiva, análise exploratória de dados e testes de associação, como o teste qui-quadrado. Essas tabelas de contingência podem ser visualizadas por meio de gráfico de barras/colunas, pois é melhor para a compreensão da distribuição conjunta das variáveis, se visualiza a frequência de ocorrências, quando se tem variáveis categóricas nominais.

library(tidyverse)
library(dplyr)
library(readxl)
library(ggplot2)
library(janitor)
library(epifitter)

Função table(): Essa função é utilizada para criar a tabela de contingência. A tabela é construída a partir das variáveis residue e species (pertencentes ao objeto survey. A função table() conta o número de ocorrências de cada combinação de categorias dessas variáveis e armazena os resultados na variável q.

survey <- read_excel("dados-diversos.xlsx","survey")
survey |>
  count(year)

# A tibble: 3 × 2
   year     n
  <dbl> <int>
1  2009   265
2  2010   216
3  2011   185

q <- table(survey$residue, survey$species)

Pacote janitor: O pacote janitor fornece funções úteis para limpeza e organização de dados, como: renomear colunas, remover valores ausentes, formatar dados em uma estrutura tabular, etc. Para dar os valores em porcentagem usa-se a função adorn_percentages(). A função tabyl() cria uma tabela de frequência tabular, mostrando a contagem de ocorrências de diferentes combinações de valores em variáveis categóricas.

#library(janitor)
survey |>
  tabyl(year, species)

 year Fgra Fspp
 2009  225   40
 2010  187   29
 2011  140   45

Visualizando os dados:

survey |>
  filter(residue != "NA") |>
  count(residue, species) |>
  ggplot(aes(residue, n, fill = species))+
  geom_col()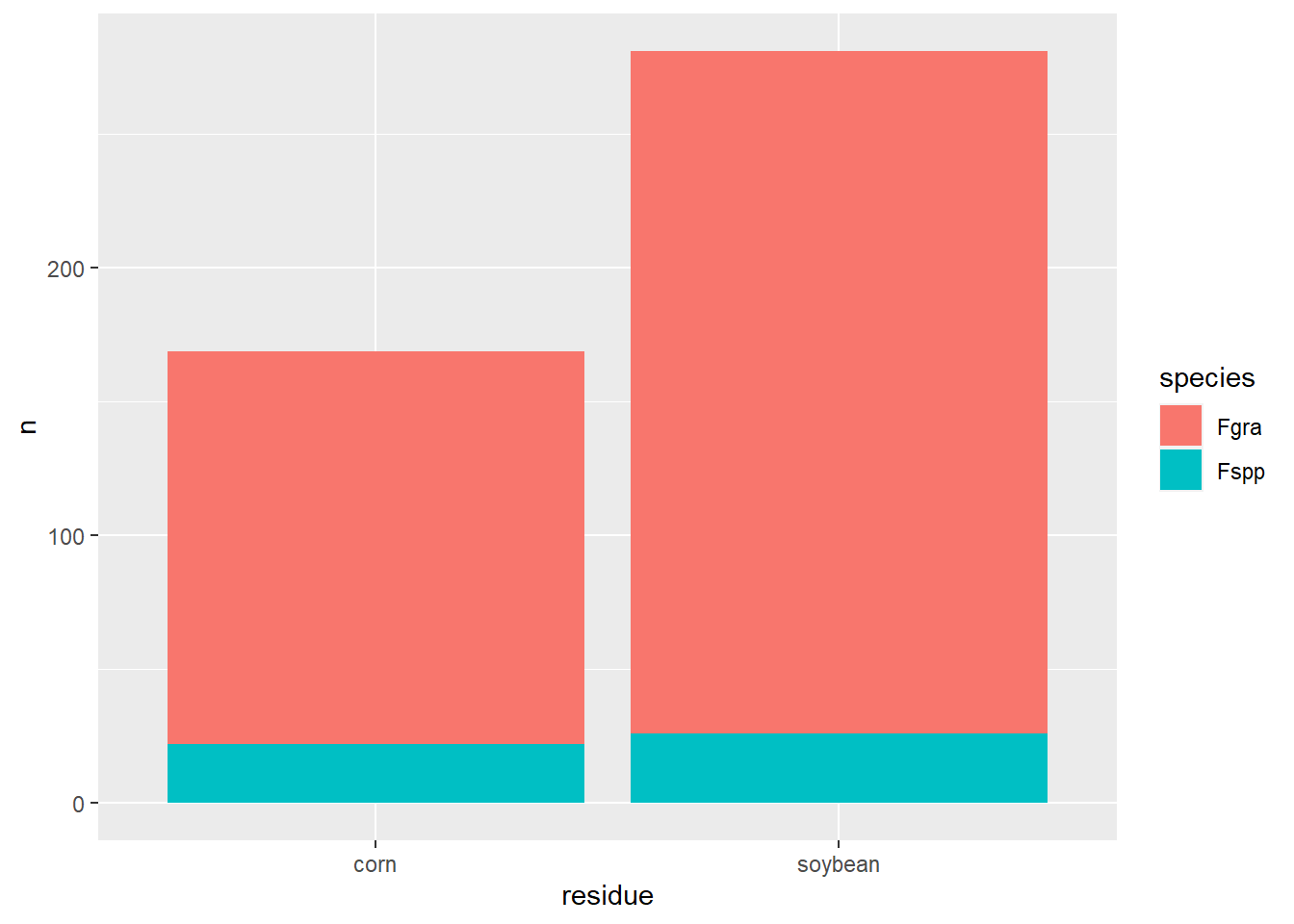

Teste qui-quadrado

O teste qui-quadrado é utilizado para avaliar a associação entre duas variáveis categóricas e quando queremos determinar se existe uma associação significativa entre elas. Este teste é baseado na comparação das frequências observadas em uma tabela de contingência com as frequências esperadas sob a hipótese nula de independência entre as variáveis. Esse teste é realizado usando a função chisq.test(), que faz parte do pacote base do R.

q <- table(survey$residue, survey$species)
chisq.test(q)


    Pearson's Chi-squared test with Yates' continuity correction

data:  q
X-squared = 1.1997, df = 1, p-value = 0.2734

Hipótese nula: as populações são iguais.

Função fisher.test(): Este teste é usado para avaliar a associação entre duas variáveis categóricas em uma tabela de contingência 2x2, ou seja, usa-se esta função quando o número de observações é baixo, algo em torno de 6 ou 7.

A severidade é influenciada pelo resíduo?

q <- table(survey$residue, survey$inc_class)
chisq.test(q)


    Pearson's Chi-squared test with Yates' continuity correction

data:  q
X-squared = 2.6165, df = 1, p-value = 0.1058

survey|>
  filter(residue != "NA") |>
  count(residue, inc_class) |>
  ggplot(aes(residue, n, fill = inc_class))+
  geom_col()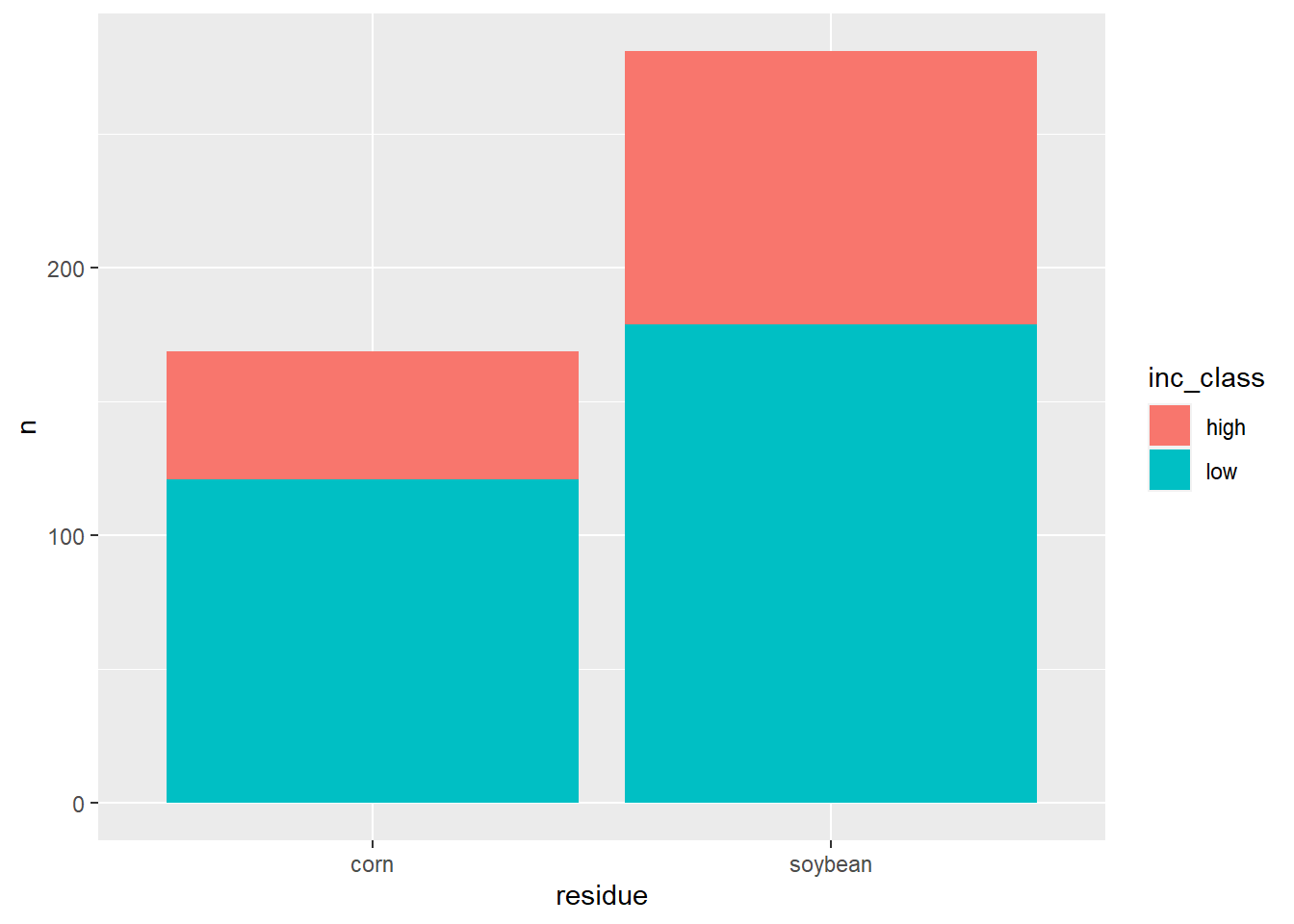

Conclusão: Pelo p valor, a classe de severidade independe do resto cultural, ou seja, o resto cultural não influencia na severidade.

Novo conjunto de dados:

curve <- read_excel("dados-diversos.xlsx", "curve")

curve2 <- curve |> 
  group_by(Irrigation, day) |>
  summarize(mean_severity = mean(severity),
            sd_severity = sd(severity))

  curve2 |>
    ggplot(aes(day, mean_severity, color = Irrigation))+
    geom_point()+
    geom_errorbar(aes(ymin = mean_severity - sd_severity, ymax = mean_severity + sd_severity, width = 0.01))+
    geom_line()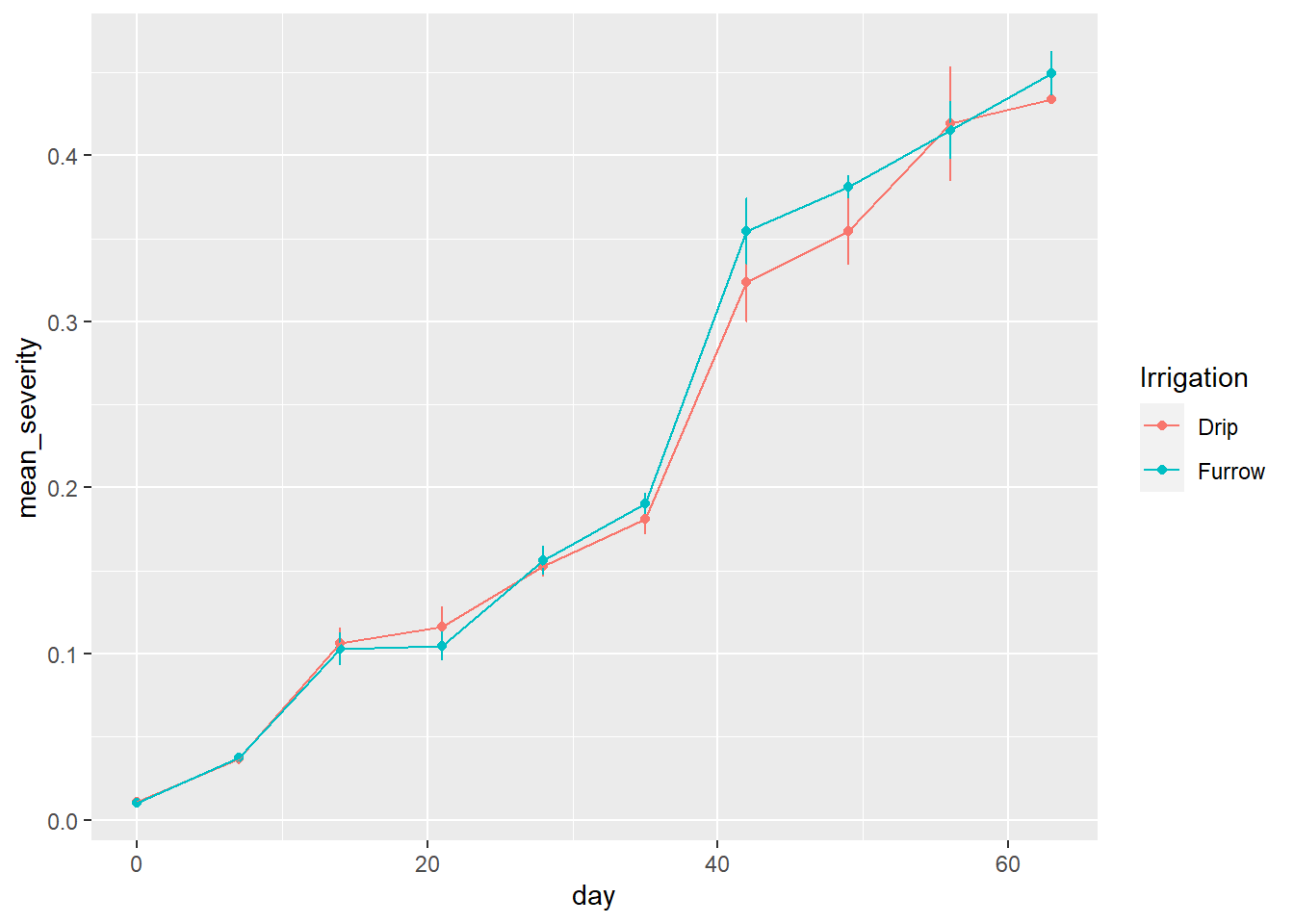

  curve3 <- curve |>
    group_by(Irrigation, rep) |>
    summarise(audpc = AUDPC(day, severity, 
                            y_proportion = F)) |>
    pivot_wider(1, names_from = Irrigation,
              values_from = audpc)
  
  t.test(curve3$Drip, curve$Furrow)


    One Sample t-test

data:  curve3$Drip
t = 51.206, df = 2, p-value = 0.0003812
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 12.26473 14.51493
sample estimates:
mean of x 
 13.38983

Exercício prático:

Carregando o conjunto de dados, mutando a variável lesion size de categórica para numerica, agrupando as variáveis e resumindo os dados:

lesion_size <- read_excel("tan-spot-wheat.xlsx", "lesion_size")

lesion2 <- lesion_size |>
mutate(lesion_size = as.numeric(lesion_size)) |>
group_by(cult, silicio, hai) |>
summarise(mean_lesion = mean(lesion_size), sd_lesion = sd(lesion_size))

Visualizando os dados graficamente:

lesion2 |>
  ggplot(aes(hai, mean_lesion, color = silicio))+
  geom_line()+
  geom_point()+
    geom_errorbar(aes(ymin = mean_lesion - sd_lesion, 
                     ymax = mean_lesion + sd_lesion), 
                     width = 0.01)+
    facet_wrap(~cult)+
  labs(y = "Lesion size (mm)",
       x = "Hours after inoculation (hai)", color = "Treatment")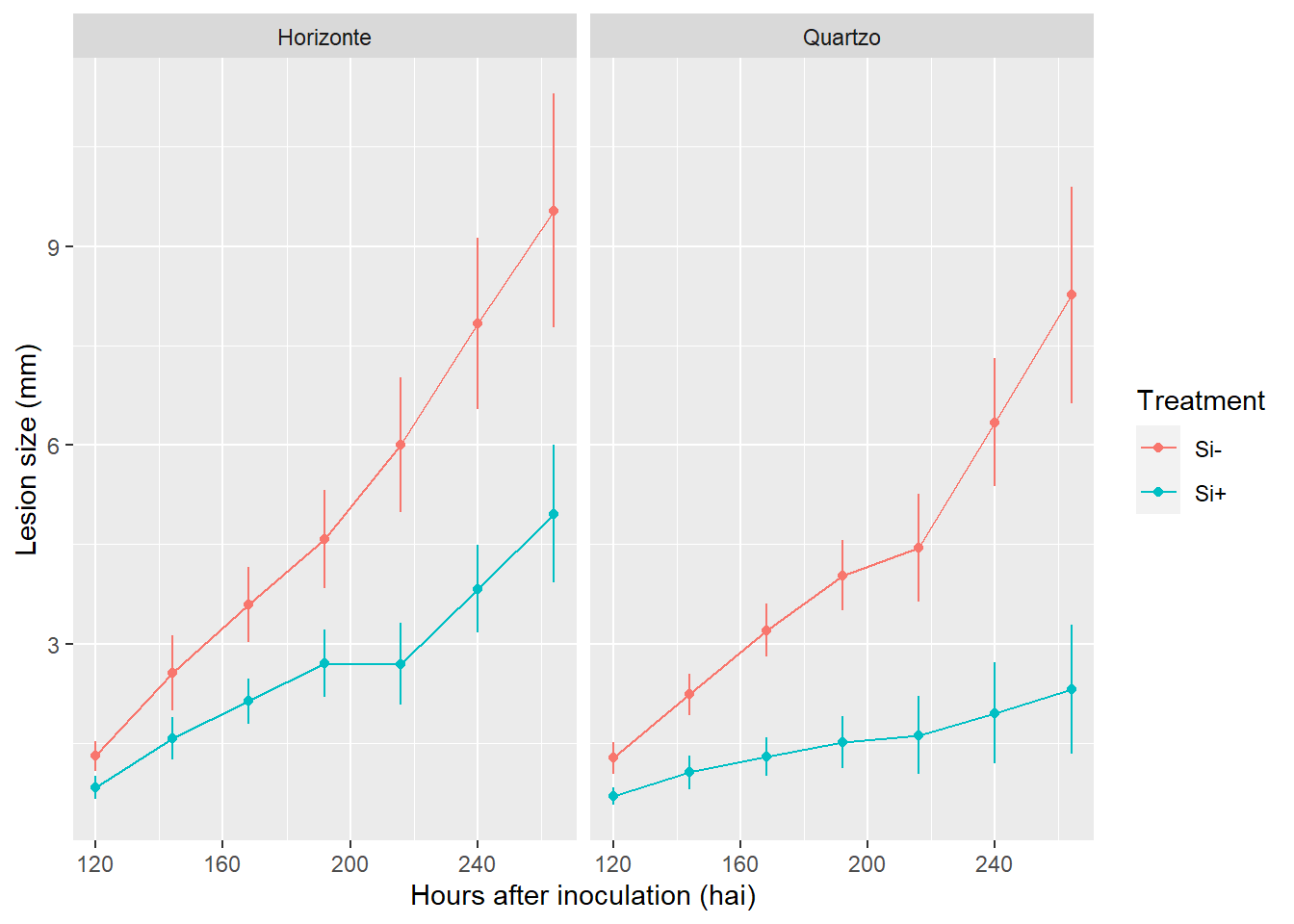

Análise de área abaixo da curva de progresso da doença - AUDPC

A AUDPC (Area Under the Disease Progress Curve) é uma medida utilizada na fitopatologia para quantificar e comparar o progresso de doenças em plantas ao longo do tempo.

A AUDPC é calculada pelos dados de observações repetidas do tamanho ou severidade da lesão em diferentes momentos. A curva do progresso da doença é plotada com o tempo no eixo x e a variável de interesse (ex. tamanho da lesão) no eixo y. A área abaixo dessa curva é então calculada para determinar AUDPC. Valores mais altos de AUDPC indicam um maior impacto da doença, enquanto valores mais baixos indicam um impacto menor.

Aplicando a AUDPC e visualizando em boxplot: Nesse bloco de comandos, calculamos a AUDPC para o tamanho da lesão com base nas informações de lesion_size, hai e nos grupos definidos pelas variáveis exp, cult, silicio e rep.

lesion3 <- lesion_size |>
  mutate(lesion_size = as.numeric(lesion_size)) |>
  group_by(exp, cult, silicio, rep) |>
  summarise(audpc = AUDPC(lesion_size, hai))

lesion3 |>
  ggplot(aes(cult, audpc, color = silicio))+
  geom_boxplot()+
  facet_wrap(~ exp)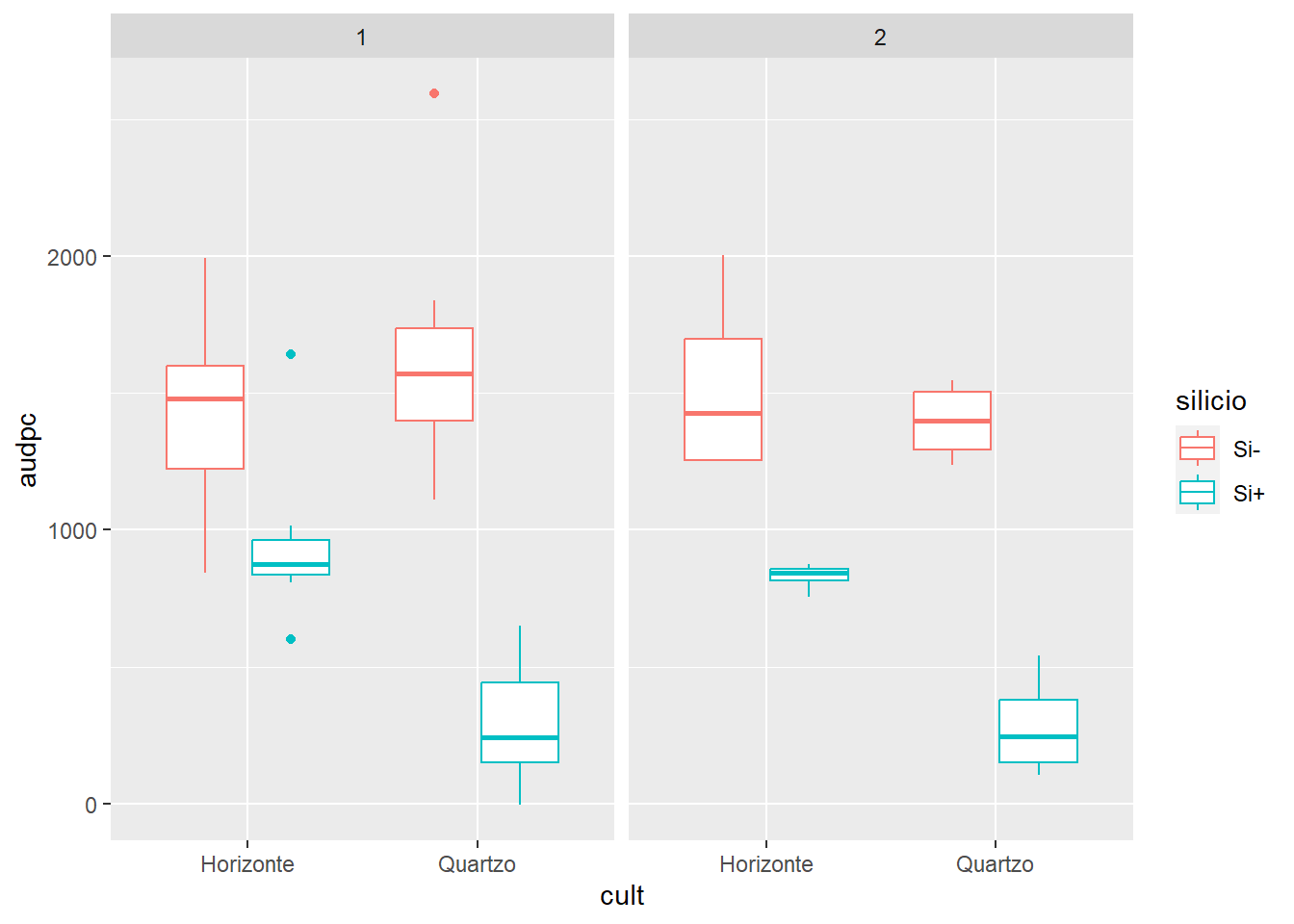

Função summarise(audpc = AUDPC(lesion_size, hai)): usamos a função summarise para calcular a AUDPC usando a função AUDPC() com as variáveis lesion_size e hai. O resultado é armazenado na nova variável audpc.

Teste ANOVA

Os resultados da análise de variância podem ajudar a identificar quais variáveis e interações têm efeito significativo na variável resposta audpc.

aov1<- aov(audpc ~ exp*cult*silicio, data = lesion3)
summary(aov1)

                 Df  Sum Sq Mean Sq F value   Pr(>F)    
exp               1   54544   54544   0.533 0.470257    
cult              1  751290  751290   7.335 0.010281 *  
silicio           1 9051552 9051552  88.377 3.15e-11 ***
exp:cult          1   36717   36717   0.359 0.553089    
exp:silicio       1      49      49   0.000 0.982615    
cult:silicio      1 1412562 1412562  13.792 0.000689 ***
exp:cult:silicio  1  143643  143643   1.403 0.244065    
Residuals        36 3687093  102419                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Se não der significativo, reduz o modelo:

aov1<- aov(audpc ~ cult*silicio, data = lesion3)
summary(aov1)

             Df  Sum Sq Mean Sq F value   Pr(>F)    
cult          1  751290  751290   7.662  0.00850 ** 
silicio       1 9051552 9051552  92.315 6.04e-12 ***
cult:silicio  1 1412562 1412562  14.406  0.00049 ***
Residuals    40 3922047   98051                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Para ver se o modelo está correto, checa as premissas.

library(performance)
check_normality(aov1)

Warning: Non-normality of residuals detected (p = 0.003).

check_heteroscedasticity(aov1)

Warning: Heteroscedasticity (non-constant error variance) detected (p = 0.040).

Se não atende as premissas, transforma os dados e verifica as médias:

aov1<- aov(sqrt(audpc) ~ cult*silicio, data = lesion3)
summary(aov1)

             Df Sum Sq Mean Sq F value   Pr(>F)    
cult          1  294.0   294.0   13.51 0.000712 ***
silicio       1 2363.9  2363.9  108.65 7.81e-13 ***
cult:silicio  1  526.5   526.5   24.20 1.62e-05 ***
Residuals    39  848.6    21.8                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
1 observation deleted due to missingness

check_normality(aov1)

OK: residuals appear as normally distributed (p = 0.146).

check_heteroscedasticity(aov1)

OK: Error variance appears to be homoscedastic (p = 0.638).

library(emmeans)

m1 <- emmeans(aov1, ~ cult | silicio, type = "response")
m1

silicio = Si-:
 cult      response    SE df lower.CL upper.CL
 Horizonte     1440 106.8 39     1233     1664
 Quartzo       1537 110.3 39     1322     1768

silicio = Si+:
 cult      response    SE df lower.CL upper.CL
 Horizonte      897  84.2 39      735     1075
 Quartzo        296  50.7 39      202      407

Confidence level used: 0.95 
Intervals are back-transformed from the sqrt scale