library(tidyverse)
library(ggplot2)
library(gsheet)
library(dplyr)Regressão não-linear e EC50
Regressão não-linear
Quando os dados não seguem um padrão linear, é necessário usar técnicas de regressão não linear para capturar a relação não linear entre as variáveis. A regressão não linear é usada quando a relação entre as variáveis independentes e dependentes não pode ser adequadamente modelada por uma função linear. Em outras palavras, quando os dados não seguem um padrão linear, é necessário usar técnicas de regressão não linear para capturar a relação não linear entre as variáveis.
Regressão não-linar para determinação de EC50:
Dados: usar o caminho do conjunto de dados sensibilidade a fungicidas, localizado na pasta do drive.
dat <- gsheet2tbl("https://docs.google.com/spreadsheets/d/15pCj0zljvd-TGECe67OMt6sa21xO8BqUgv4d-kU8qi8/edit#gid=0")Trabalhando os dados:
options(scipen=999)
dat2 <- dat |>
dplyr::select(-Isolate, Population) |>
group_by(Code, Year, Dose) |>
summarise(GC_mean = mean(GC))O comando options(scipen=999) define a opção scipen para o valor 999. A opção scipen é usada para controlar a exibição de números científicos em notação exponencial. Definir scipen como 999 desativa a notação exponencial e exibirá os números completos.
Esse bloco de comandos realiza uma sequência de operações no dataframe dat: Remove as colunas “Isolate” e “Population” (a coluna “Isolate” e a coluna “Population” não estarão presentes no resultado dat2). Agrupa os dados restantes por “Code”, “Year” e “Dose”. Calcula a média da coluna “GC” para cada grupo e armazena os resultados na coluna “GC_mean” em um novo dataframe chamado date, ou seja, summarise(GC_mean = mean(GC)) está sendo utilizado para calcular a média da coluna “GC” dentro de cada grupo definido pelas colunas “Code”, “Year” e “Dose”. A média resultante é atribuída a uma nova coluna chamada “GC_mean” no dataframe resultante.
Para fazer um gráfico só com um dos isolados:
FGT152 <- dat2 |>
filter(Code == "FGT152")
FGT152 |>
ggplot(aes(factor(Dose), GC_mean))+
geom_point()+
geom_line()+
facet_wrap(~ Code)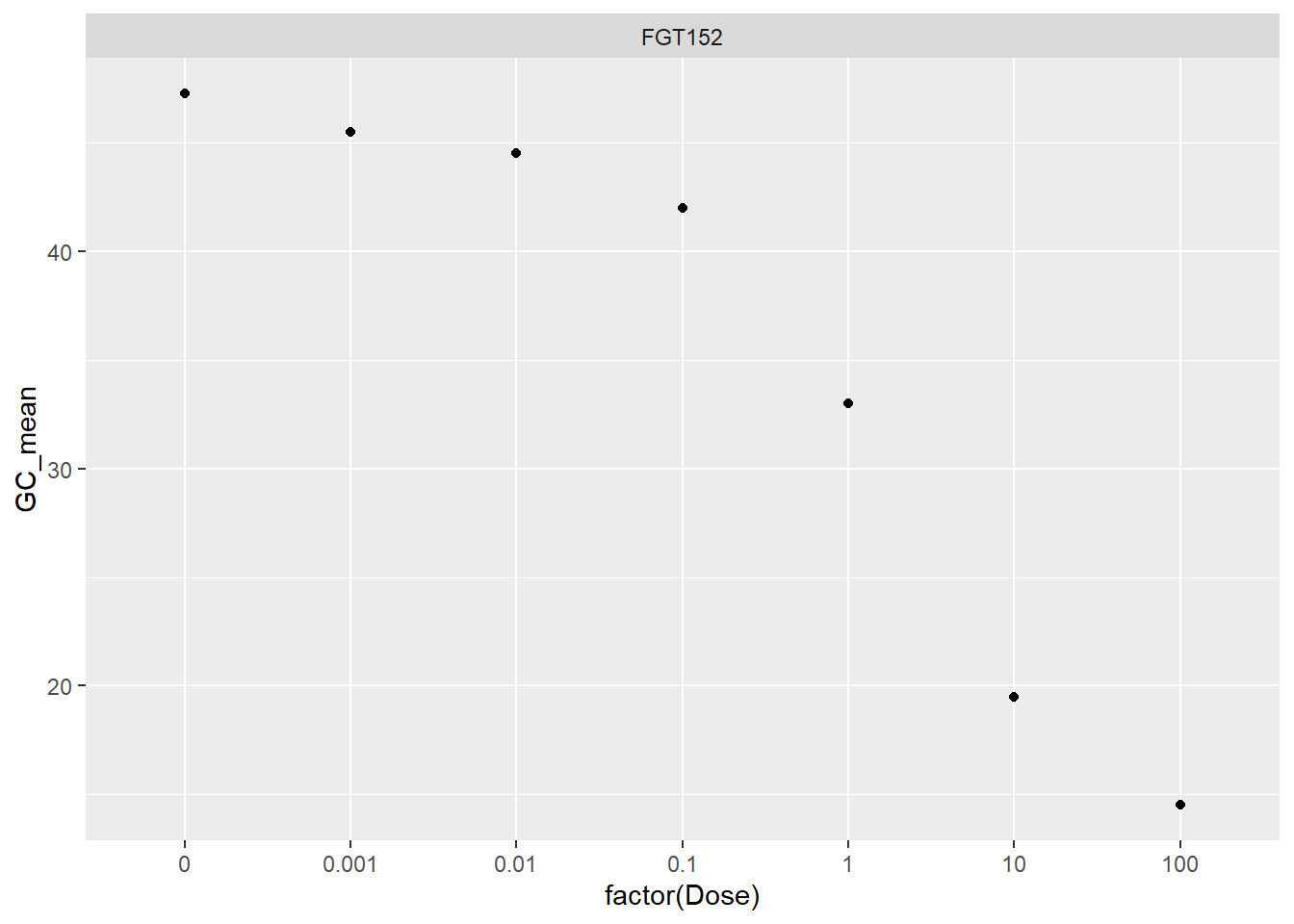
Criou-se um gráfico usando o dataframe FGT152, que é um subconjunto dos dados filtrados do dat2. O gráfico mostra os valores de “GC_mean” em relação a “Dose” para o código “FGT152”, com pontos e uma linha contínua. Os painéis separados são criados para cada nível único de “Code”, mas neste caso, como só há “FGT152”, há apenas um painel.
EC50 com pacote DRC
O pacote DRC é especialmente útil para ajustar modelos de regressão dose-resposta e realizar análises estatísticas relacionadas. Ele oferece modelos para ajustar curvas de dose-resposta, incluindo modelos log-logísticos, log-probit, Weibull, etc. O pacote fornece funções para calcular estimativas de EC50.
Modelos
Modelo log.logistico3: o modelo de três parâmetros log-logístico descreve a relação entre a dose de um agente ou tratamento e a resposta biológica. Esse modelo assume uma resposta crescente ou decrescente com a dose e é frequentemente usado quando se espera uma resposta em forma de curva em S ou uma resposta em forma de S invertido.
library(drc)
drc1 <- drm(GC_mean ~ Dose, data = FGT152,
fct = LL.3())
AIC(drc1)[1] 33.60846summary(drc1)
Model fitted: Log-logistic (ED50 as parameter) with lower limit at 0 (3 parms)
Parameter estimates:
Estimate Std. Error t-value p-value
b:(Intercept) 0.401905 0.053427 7.5225 0.001672 **
d:(Intercept) 47.540342 1.459890 32.5643 0.000005302 ***
e:(Intercept) 7.220130 2.340119 3.0854 0.036739 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error:
1.993805 (4 degrees of freedom)plot(drc1)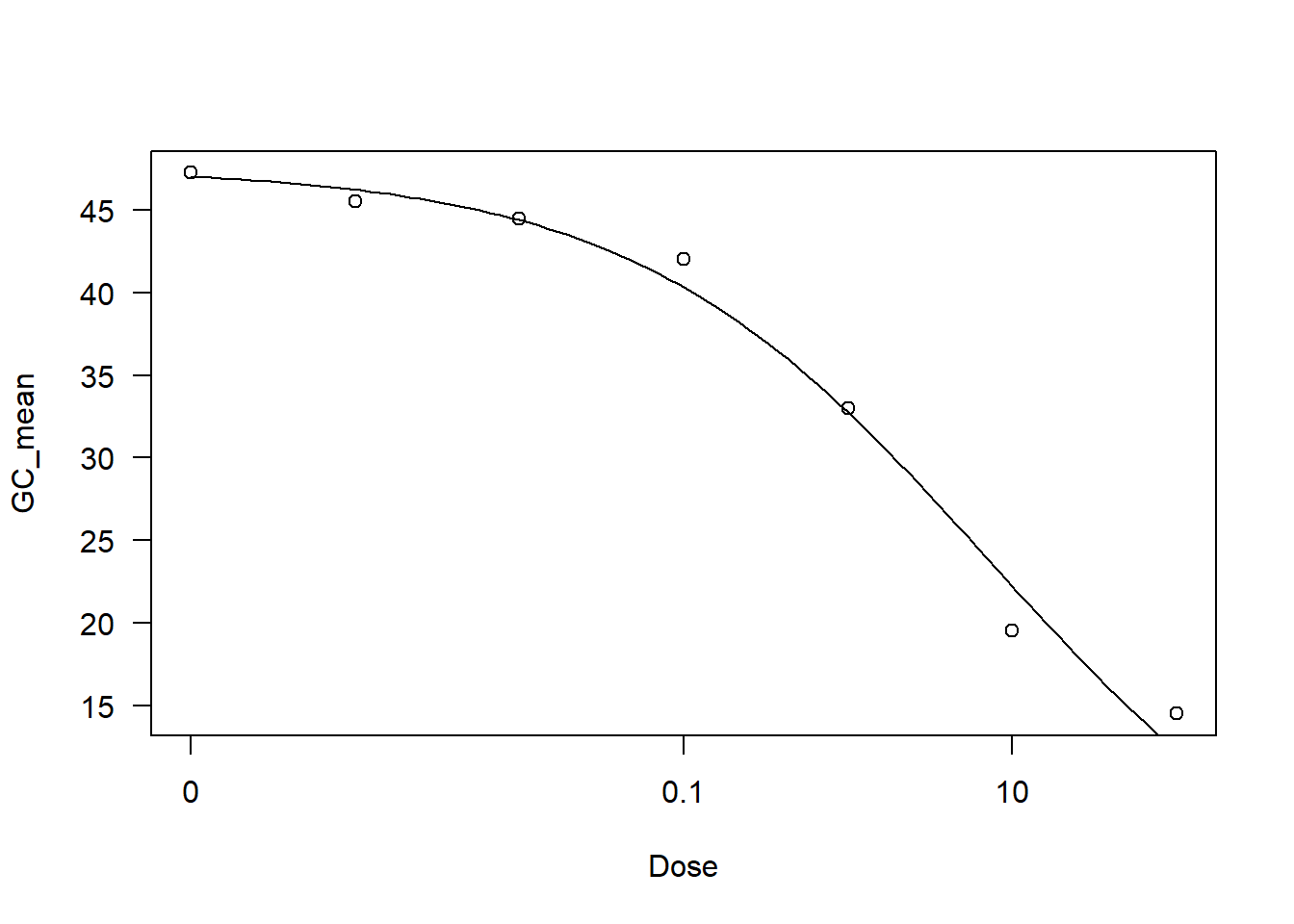
ED(drc1, 50)
Estimated effective doses
Estimate Std. Error
e:1:50 7.2201 2.3401O comando drc1 <- drm(GC_mean ~ Dose, data = FGT152, fct = LL.3()) : esses comandos são utilizados para ajustar um modelo de regressão de dose-resposta usando a função drm() da biblioteca ‘drc’ (dose-response modeling). O argumento GC_mean ~ Dose especifica que a variável resposta é “GC_mean” e a variável preditora é “Dose”. O argumento data = FGT152 indica que os dados para ajuste do modelo são provenientes do dataframe FGT152. O argumento fct = LL.3() especifica o tipo de modelo a ser ajustado, neste caso, um modelo de três parâmetros log-logístico (LL.3()). AIC(drc1) é a função que utilizamos para calcular o AIC para o modelo ajustado. O AIC é uma medida que avalia a qualidade relativa do modelo, considerando a qualidade do ajuste e a complexidade do modelo. Quanto menor o valor do AIC, melhor o ajuste. A função ED(drc1, 50): calcula a dose efetiva (ED) para um determinado nível de resposta, neste caso, 50%. O comando ED() é usado para calcular as doses efetivas para um modelo de regressão de dose-resposta. O argumento drc1 especifica o modelo ajustado e o argumento 50 indica o nível de resposta desejado (50% neste caso).
Modelo W1.3: tem melhor ajuste atraves do AIC. Esse modelo permite uma maior flexibilidade na modelagem da forma da curva de resposta em relação à dose, pois inclui o parâmetro de assimetria (g). Esse parâmetro permite que a curva de resposta seja assimétrica, podendo assumir formas como curvas em forma de S assimétricas.
drc1 <- drm(GC_mean ~ Dose, data = FGT152,
fct = W1.3())
AIC(drc1)[1] 37.75192summary(drc1)
Model fitted: Weibull (type 1) with lower limit at 0 (3 parms)
Parameter estimates:
Estimate Std. Error t-value p-value
b:(Intercept) 0.28354 0.04760 5.9567 0.003987 **
d:(Intercept) 48.38112 2.09996 23.0390 0.00002103 ***
e:(Intercept) 30.12379 12.58003 2.3946 0.074796 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error:
2.680509 (4 degrees of freedom)plot(drc1)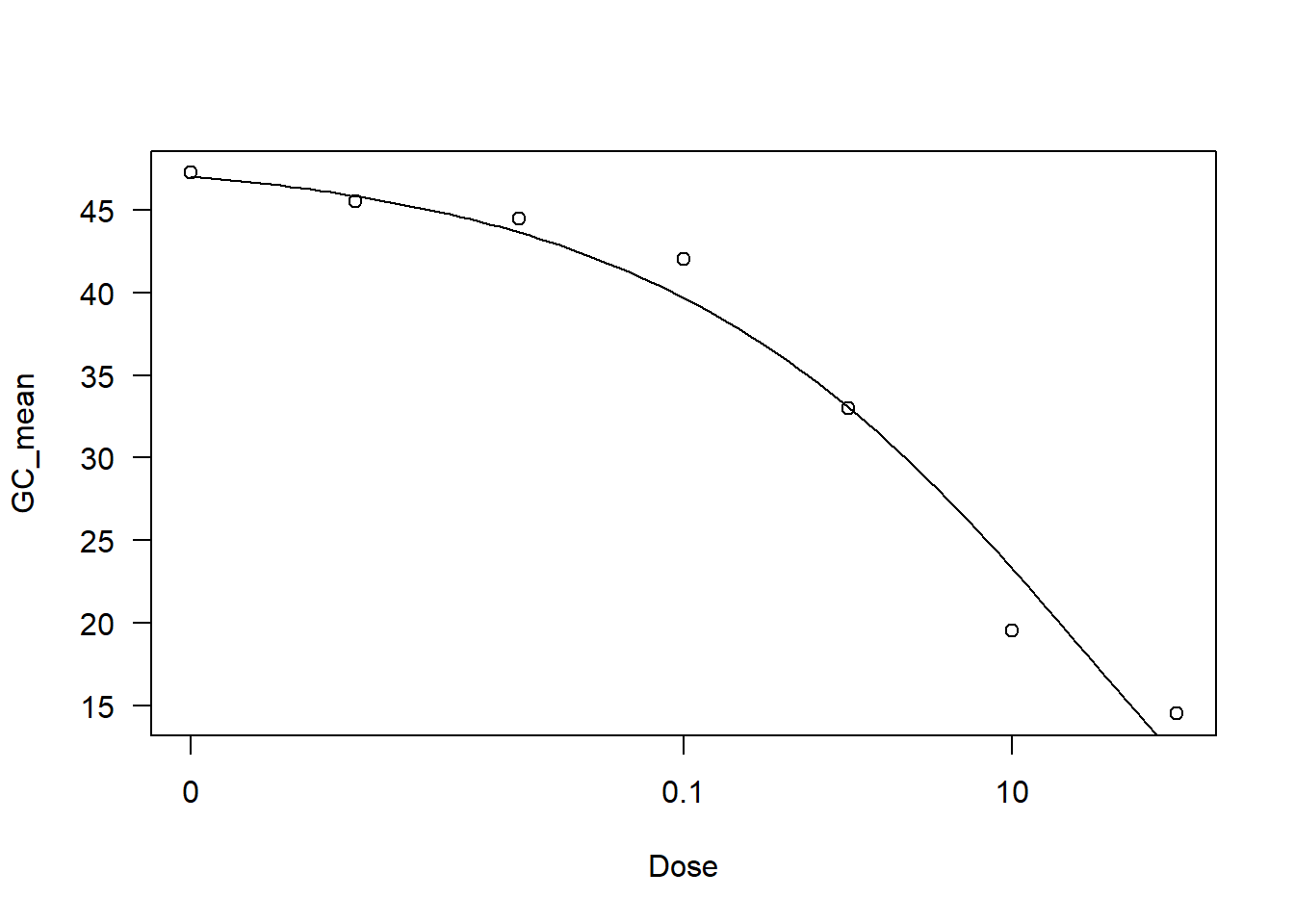
ED(drc1, 50)
Estimated effective doses
Estimate Std. Error
e:1:50 8.2704 3.6719Pacote ec50estimator
Fornece os valores de EC50 para os dados. É útil para comparar as estimativas de EC50 entre diferentes identificadores (ID) e identificar possíveis diferenças na resposta à dose.
library(ec50estimator)
df_ec50 <- estimate_EC50(GC_mean ~ Dose,
data = dat2,
isolate_col = "Code",
interval = "delta",
fct = drc::LL.3())
df_ec50 |>
ggplot(aes(Estimate, reorder(ID, Estimate)))+
geom_point()+
geom_errorbar(aes(xmin = Lower,
xmax = Upper), width = 0.1)+
xlim(0,30)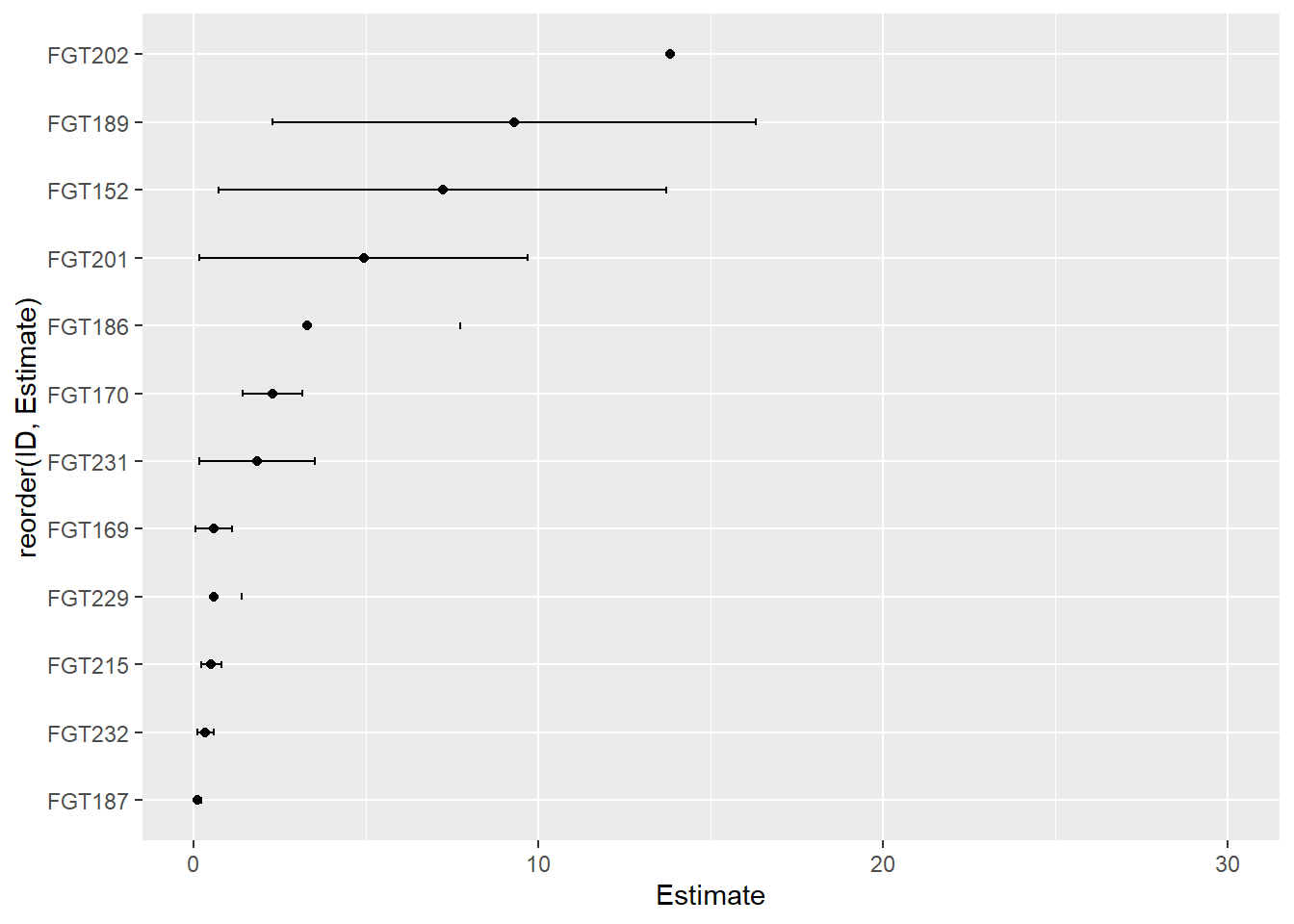
A função estimate_EC50() é utilizada para estimar os valores de EC50 a partir dos dados. Dentro dessa função são usados varios argumentos, esses argumentos possuem diferentes papeis na função: O isolate_col = “Code” foi usado para definir a coluna “Code” como uma coluna de identificação única para diferentes amostras. O interval = “delta” define o tipo de intervalo de confiança que deverá ser calculado para as estimativas de EC50. o comando fct = drc::LL.3() especifica o modelo de ajuste, neste caso, o modelo de três parâmetros log-logístico. Dentro do ggplot e da função aes o argumento (Estimate, reorder(ID, Estimate)) especifica as variáveis a serem mapeadas nos eixos x e y do gráfico. “Estimate” corresponde aos valores estimados de EC50 e “ID” é reordenado de acordo com os valores de Estimate para controlar a ordem no gráfico. Nesse caso, a função geom_errorbar adiciona barras de erro ao gráfico, utilizando os valores inferiores (Lower) e superiores (Upper) dos intervalos de confiança das estimativas de EC50. O xlim(0,30) define os limites do eixo x do gráfico, limitando o intervalo de visualização das estimativas até 30.